Parallelizing SGD

Parallelized Stochastic Gradient Descent
Hogwild!
Downpour SGD
Parallelized Stochastic Gradient Descent
Parallelized Stochastic Gradient Descent

算法步骤:

将训练数据集$D$负载均衡地划分为$c$个子集: $D=\bigcup_{i=1}^{c}D_i$,其中$\left|D_1\right|=\left|D_2\right|=\left|D_3\right|=…=\left|D_c\right|=T$,并将子集$D_i$分配到第i台机器.
在每台机器上，给定学习率$\eta$,并令向量$v:=0$.
对于$i\in\left\{ 1,2,…,c \right\} $,并行地执行:
1. 将$D_i$中的元素随机打乱,设得到的样本序列为$ \left\{ \tilde{x}_j , \tilde{y}_j \right\}^T_{j=1}$
2. 初始化$w_0^{(i)}:=v$.
3. 按照以下循环更新参数.
  FOR $j = 1,2,…,T$ DO
  {
  $\quad\quad w_j^{(i)} = w_{j-1}^{(i)}-\eta\left. \frac{\partial l(x_i, y_i,w)}{\partial w}\right|_{(\tilde{x}_j , \tilde{y}_j , {w_{j-1}^{(i)}})}$
  }
通过全归约操作,使每台机器获得平均权值向量$v=\frac{1}{c} \sum_{k=1}^c w_T^{(i)}$
若达到收敛准则,则算法结束,返回$v$;否则,转至3.

算法只涉及数据并行,没有模型并行(每台机器上都有一份完整的模型参数$w$),因此它适合于模型参数量相对较小,而训练数据集相对较大的情形.每台机器各自负责一个本地数据块的计算,计算完成后,执行一次通信(step 4),获取更新后的值.

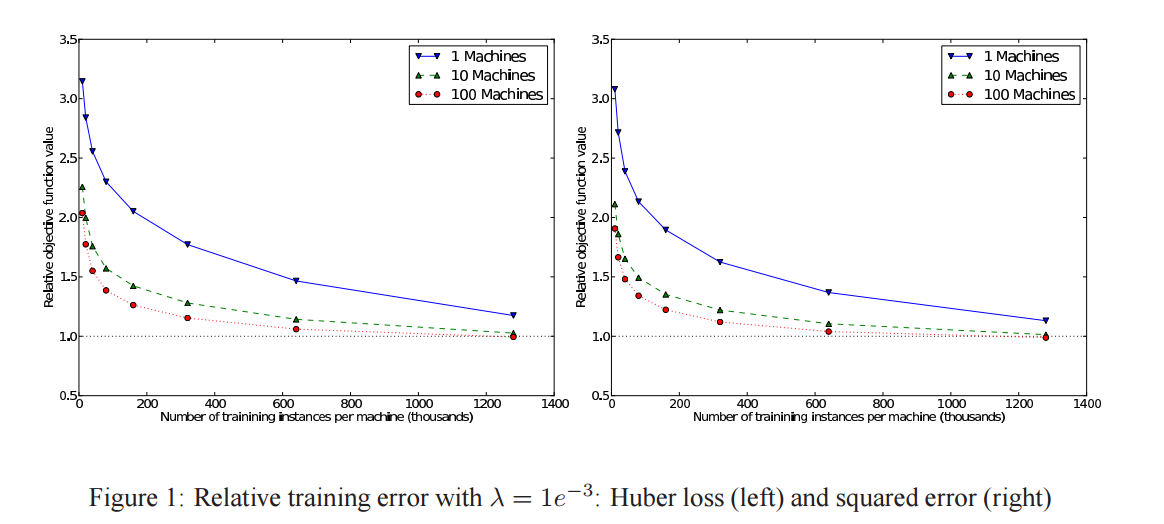
Hogwild!

Hogwild!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent

Niu提出了被称为Hogwild的并行SGD方法。该方法在多个CPU时间进行并行。处理器通过共享内存来访问参数，并且这些参数不进行加锁。它为每一个cpu分配不重叠的一部分参数（分配互斥），每个cpu只更新其负责的参数。该方法只适合处理数据特征是稀疏的。该方法几乎可以达到一个最优的收敛速度，因为cpu之间不会进行相同信息重写。

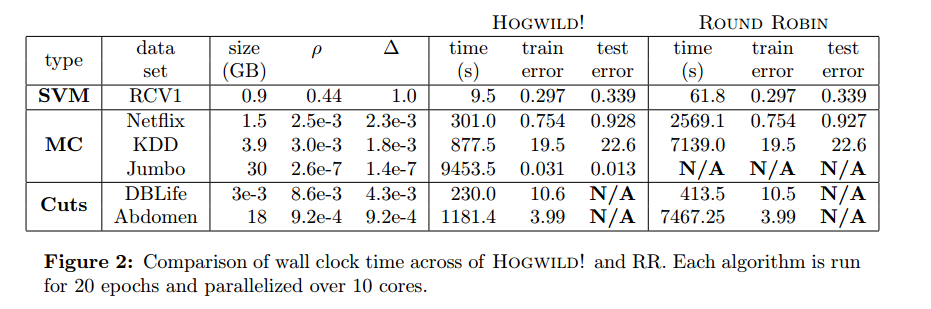
Downpour SGD

Large Scale Distributed Deep Networks

Downpour SGD 是 Dean et al. 4在 Google 的 DistBelief 框架中使用的一个异步 SGD 的变种（TensorFlow 的前身）。它在训练数据的子集上并行运行多个模型的复制。它们会把自己的更新发送到一个参数服务器上，而完整的参数被分发到许多的机器上。每个机器负责一小部分的模型参数的存储和更新。然而，因为各个复制模型直接并没有通信，即分享权重或者更新，它们的参数会持续遇到发散、妨碍收敛的问题。
请见:Downpour SGD

Parallelized Stochastic Gradient Descent

Hogwild!

Downpour SGD