Java中Math.exp的近似算法

发表于   |   分类于   |  

实验过程中发现Java的Math.exp()操作特别耗时间,在坐标下降求解Logistic Regression的过程中Math.exp()几乎用到了70%的时间,因此我们思考是否可以通过近似的方法计算$e^x$的值,文中整理了两种实用的近似计算Math.exp()方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/**
* Take <em>e</em><sup>a</sup>.  The opposite of <code>log()</code>. If the
* argument is NaN, the result is NaN; if the argument is positive infinity,
* the result is positive infinity; and if the argument is negative
* infinity, the result is positive zero.
*
* @param x the number to raise to the power
* @return the number raised to the power of <em>e</em>
* @see #log(double)
* @see #pow(double, double)
*/
public static double exp(double x)
{
	if (x != x)
		return x;
	if (x > EXP_LIMIT_H)
		return Double.POSITIVE_INFINITY;
	if (x < EXP_LIMIT_L)
		return 0;
		
	// Argument reduction.
	double hi;
	double lo;
	int k;
	double t = abs(x);
	if (t > 0.5 * LN2)
	{
		if (t < 1.5 * LN2)
		{
			hi = t - LN2_H;
			lo = LN2_L;
			k = 1;
		}
		else
		{
			k = (int) (INV_LN2 * t + 0.5);
			hi = t - k * LN2_H;
			lo = k * LN2_L;
		}
		if (x < 0)
		{
			hi = -hi;
			lo = -lo;
			k = -k;
		}
		x = hi - lo;
	}
	else if (t < 1 / TWO_28)
		return 1;
	else
		lo = hi = k = 0;
	
	// Now x is in primary range.
	t = x * x;
	double c = x - t * (P1 + t * (P2 + t * (P3 + t * (P4 + t * P5))));
	if (k == 0)
		return 1 - (x * c / (c - 2) - x);
	double y = 1 - (lo - x * c / (2 - c) - hi);
	return scale(y, k);
}

可以看到Java的Math.exp()操作是比较复杂的,自然所消耗的时间也会比较多,然而对于一些对Math.exp()的精度要求不是特别高但操作数量巨大的应用而言,精度较高但复杂度同时较高的Math.exp算法就显得有些力不从心了。
本文整理了两种近似计算exp()的算法：

算法一 使用浮点型表示的特性

算法如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
static double[] ExpAdjustment = new double[256] {
	1.040389835,
	1.039159306,
	1.037945888,
	1.036749401,
	1.035569671,
	1.034406528,
	1.033259801,
	1.032129324,
	1.031014933,
	1.029916467,
	1.028833767,
	1.027766676,
	1.02671504,
	1.025678708,
	1.02465753,
	1.023651359,
	1.022660049,
	1.021683458,
	1.020721446,
	1.019773873,
	1.018840604,
	1.017921503,
	1.017016438,
	1.016125279,
	1.015247897,
	1.014384165,
	1.013533958,
	1.012697153,
	1.011873629,
	1.011063266,
	1.010265947,
	1.009481555,
	1.008709975,
	1.007951096,
	1.007204805,
	1.006470993,
	1.005749552,
	1.005040376,
	1.004343358,
	1.003658397,
	1.002985389,
	1.002324233,
	1.001674831,
	1.001037085,
	1.000410897,
	0.999796173,
	0.999192819,
	0.998600742,
	0.998019851,
	0.997450055,
	0.996891266,
	0.996343396,
	0.995806358,
	0.995280068,
	0.99476444,
	0.994259393,
	0.993764844,
	0.993280711,
	0.992806917,
	0.992343381,
	0.991890026,
	0.991446776,
	0.991013555,
	0.990590289,
	0.990176903,
	0.989773325,
	0.989379484,
	0.988995309,
	0.988620729,
	0.988255677,
	0.987900083,
	0.987553882,
	0.987217006,
	0.98688939,
	0.98657097,
	0.986261682,
	0.985961463,
	0.985670251,
	0.985387985,
	0.985114604,
	0.984850048,
	0.984594259,
	0.984347178,
	0.984108748,
	0.983878911,
	0.983657613,
	0.983444797,
	0.983240409,
	0.983044394,
	0.982856701,
	0.982677276,
	0.982506066,
	0.982343022,
	0.982188091,
	0.982041225,
	0.981902373,
	0.981771487,
	0.981648519,
	0.981533421,
	0.981426146,
	0.981326648,
	0.98123488,
	0.981150798,
	0.981074356,
	0.981005511,
	0.980944219,
	0.980890437,
	0.980844122,
	0.980805232,
	0.980773726,
	0.980749562,
	0.9807327,
	0.9807231,
	0.980720722,
	0.980725528,
	0.980737478,
	0.980756534,
	0.98078266,
	0.980815817,
	0.980855968,
	0.980903079,
	0.980955475,
	0.981017942,
	0.981085714,
	0.981160303,
	0.981241675,
	0.981329796,
	0.981424634,
	0.981526154,
	0.981634325,
	0.981749114,
	0.981870489,
	0.981998419,
	0.982132873,
	0.98227382,
	0.982421229,
	0.982575072,
	0.982735318,
	0.982901937,
	0.983074902,
	0.983254183,
	0.983439752,
	0.983631582,
	0.983829644,
	0.984033912,
	0.984244358,
	0.984460956,
	0.984683681,
	0.984912505,
	0.985147403,
	0.985388349,
	0.98563532,
	0.98588829,
	0.986147234,
	0.986412128,
	0.986682949,
	0.986959673,
	0.987242277,
	0.987530737,
	0.987825031,
	0.988125136,
	0.98843103,
	0.988742691,
	0.989060098,
	0.989383229,
	0.989712063,
	0.990046579,
	0.990386756,
	0.990732574,
	0.991084012,
	0.991441052,
	0.991803672,
	0.992171854,
	0.992545578,
	0.992924825,
	0.993309578,
	0.993699816,
	0.994095522,
	0.994496677,
	0.994903265,
	0.995315266,
	0.995732665,
	0.996155442,
	0.996583582,
	0.997017068,
	0.997455883,
	0.99790001,
	0.998349434,
	0.998804138,
	0.999264107,
	0.999729325,
	1.000199776,
	1.000675446,
	1.001156319,
	1.001642381,
	1.002133617,
	1.002630011,
	1.003131551,
	1.003638222,
	1.00415001,
	1.004666901,
	1.005188881,
	1.005715938,
	1.006248058,
	1.006785227,
	1.007327434,
	1.007874665,
	1.008426907,
	1.008984149,
	1.009546377,
	1.010113581,
	1.010685747,
	1.011262865,
	1.011844922,
	1.012431907,
	1.013023808,
	1.013620615,
	1.014222317,
	1.014828902,
	1.01544036,
	1.016056681,
	1.016677853,
	1.017303866,
	1.017934711,
	1.018570378,
	1.019210855,
	1.019856135,
	1.020506206,
	1.02116106,
	1.021820687,
	1.022485078,
	1.023154224,
	1.023828116,
	1.024506745,
	1.025190103,
	1.02587818,
	1.026570969,
	1.027268461,
	1.027970647,
	1.02867752,
	1.029389072,
	1.030114973,
	1.030826088,
	1.03155163,
	1.032281819,
	1.03301665,
	1.033756114,
	1.034500204,
	1.035248913,
	1.036002235,
	1.036760162,
	1.037522688,
	1.038289806,
	1.039061509,
	1.039837792,
	1.040618648
};
static double FastExp(double x)
{
	var tmp = (long)(1512775 * x + 1072632447);
	int index = (int)(tmp >> 12) & 0xFF;
	return BitConverter.Int64BitsToDouble(tmp << 32) * ExpAdjustment[index];
}

算法二: 使用Lookup Table直接查表

使用$e^{3.45}=e^{3}\times e^{0.4}\times e^{0.05}$的性质可以进行如下近似:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public void preCompute(){
       for(int i = 0; i < 5; i++){
           double l = Math.pow(10, -2*i);
           for(int j = 0; j < 100; j++){
               expTable[i][j] = Math.exp(j * l);
           }
       }
}
public double exp(double val) {
	double result = 1.0;
	int bitNum = 0;
	for(int i = 0; i < 3; i++){
		bitNum = (int)val % 100;
		if(bitNum >= 0) {
			result *= expTable[i][bitNum];
		}else{
			result /= expTable[i][-bitNum];
		}
		val*= 100;
	}
	return result;
}

但算法二的缺点在于只能计算有限范围内$e^x$的值,如果需要计算的$e^x$的x值很大的话可能表会很大,同时其相对误差也可能会比较大,下面会详细些比较二者的差别：

近似算法比较

效率

我们对精确算法、模拟算法1、模拟算法2进行了对比,在服务器上依次运行100,000,000次三种算法,可以得到:

1
2
3
4
空操作 4578  ms
精确解 15756 ms
算法一 5623 ms
算法二 6656 ms

可以看到,近似算法跟精确解相比时间上大大缩短,可以有2-3倍的效率提升。

准确度

算法一跟算法二都具有比较好的准确度,下图是两种近似算法的准确度图,从下图可以看到二者都具有比较高的准确度,算法一的误差率在0.6%内,算法二的误差率在1%内。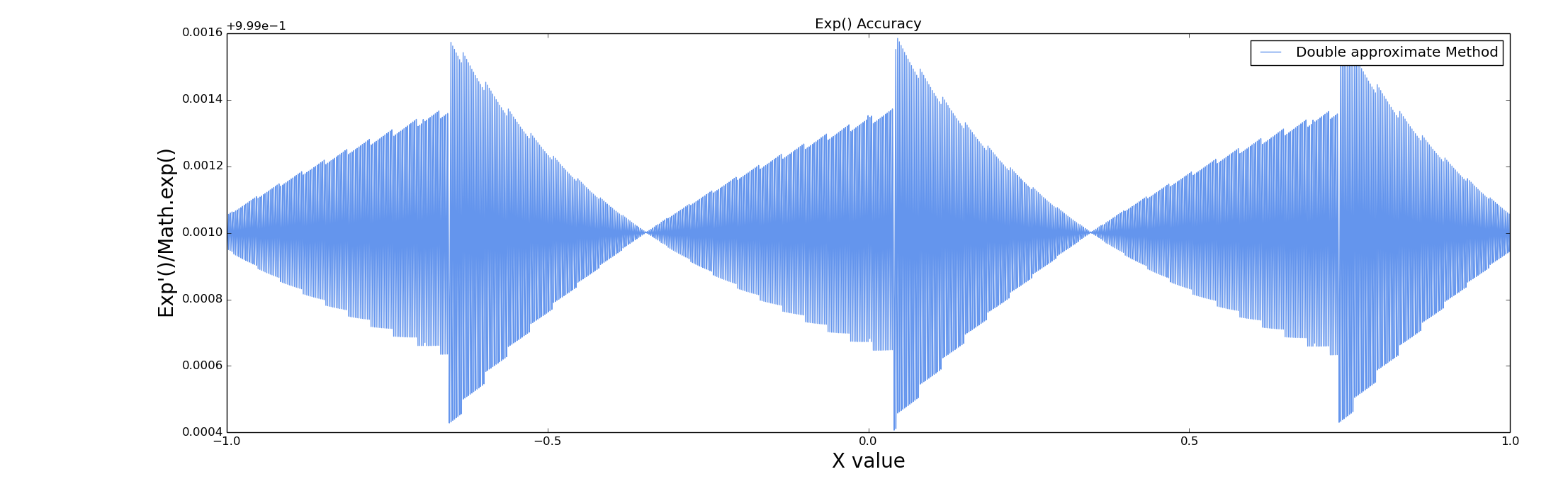
算法1准确度
算法2准确度
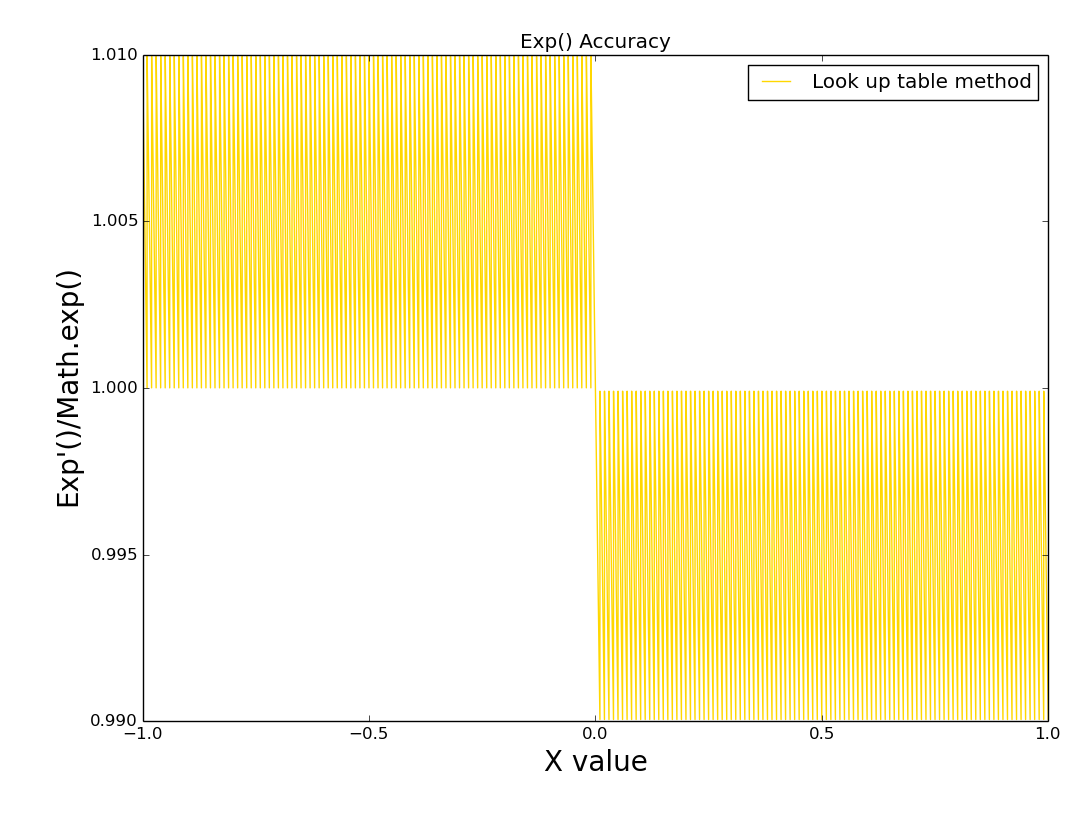
当然,有理论证明,算法一最差的误差率在4%(在某些特殊的值下),算法二最差的误差率在$5\times 10^{-8}%$内(如果存在[1,0,1,…,$10^{-10}$]的lookup table),可以证明,如果存在$10^{-a}$的lookuptable,那么误差率在$[-5\times[(10^{-(a+1)}-1],5\times[(10^{-(a+1)}-1]]$内。
更大的Lookup table会导致更多的时间消耗,但会更好；但由于误差率的计算是Exp’(x)/exp(x)，因此当计算x为负数时，exp(x)的准确值较小，相对误差会比较大。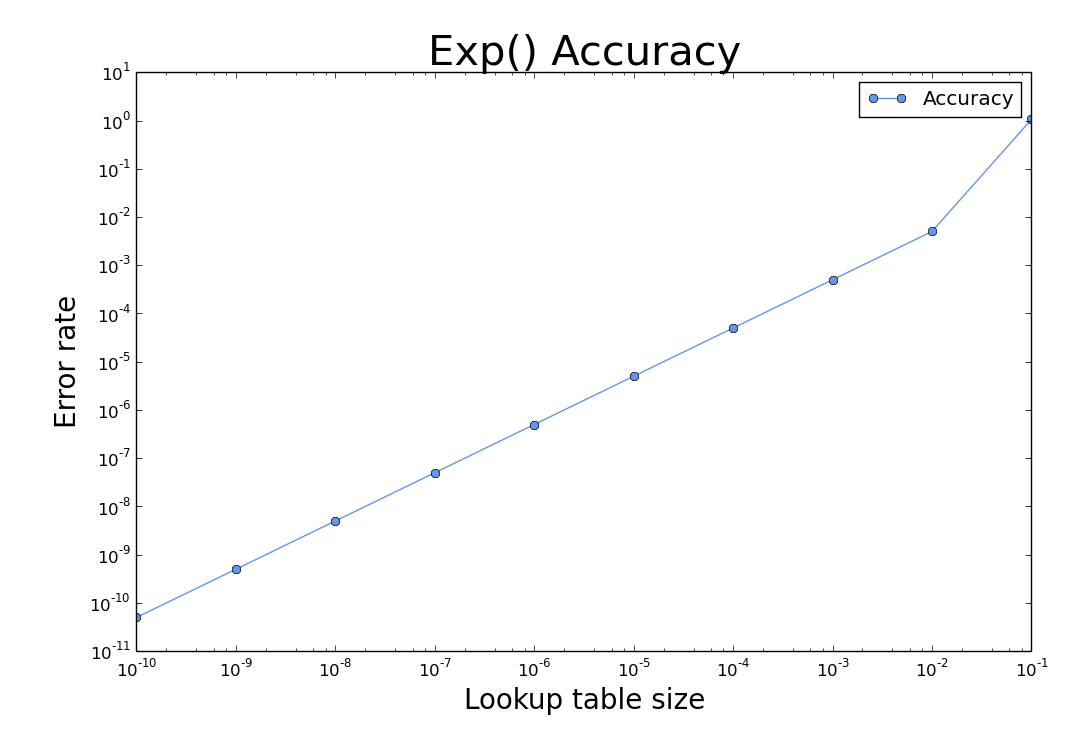
算法2准确度与表大小的关系

总结

综上,文章整理了两种近似计算exp()的算法,各有利弊,其中算法一基于Double的表示形式,同时辅助以ExpAdjustment[]数组,绝大部分点的误差率都在0.6%以内,不过在因为ExpAdjustment[]调节的值有限,算法一的最坏误差率在4%左右；而算法二的误差率可以通过lookup Table表的大小调节,误差率比较小,缺点是适用于若干有限值的计算(lookup table的大小有限)。

同时还发现存在pow的近似算法(Optimized pow() approximation for Java, C / C++, and C#),

1
2
3
4
5
public static double pow(final double a, final double b) {
	final long tmp = Double.doubleToLongBits(a);
    final long tmp2 = (long)(b * (tmp - 4606921280493453312L)) + 4606921280493453312L;
    return Double.longBitsToDouble(tmp2);
}

可以比Math.pow()快23倍(Intel Core2 Quad, Q9550, Java 1.7.0_01-b08, 64-Bit Server V)。误差率5%-12%,极端情况可以达到25%。

参考:
http://martin.ankerl.com/tag/floating-point/
https://gist.github.com/mratkovic/b273376496bb283c9dec
http://ideone.com/fork/UwNgx
http://developer.classpath.org/doc/java/lang/StrictMath-source.html