A brief introduction to stochastic gradient descent and its variants.
SGD模型
SGD指stochastic gradient descent, 即随机梯度下降,是梯度下降的batch版本.
对于训练数据集,我们首先将其分成n个batch,每个batch包含m个样本。我们每次更新都利用一个batch的数据,而非整个训练集。即:
\begin{equation}
\theta = \theta - \eta \cdot \nabla_\theta J( \theta; x^{(i)}; y^{(i)})
\end{equation}
其中, $\eta$ 为学习率,$g_t$为$x$在$t$时刻的梯度。
这么做的好处在于:
- 当训练数据太多时,利用整个数据集更新往往时间上不显示。batch的方法可以减少机器的压力,并且可以更快地收敛。
- 当训练集有很多冗余时(类似的样本出现多次),batch方法收敛更快。以一个极端情况为例,若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch,后一半作为另一个batch,那么在一次遍历训练集时,batch的方法向最优解前进两个step,而整体的方法只前进一个step。
缺点:(正因为有这些缺点才让这么多大神发展出了后续的各种算法)
- 选择合适的learning rate比较困难 - 对所有的参数更新使用同样的learning rate。对于稀疏数据或者特征,有时我们可能想更新快一些对于不经常出现的特征,对于常出现的特征更新慢一些,这时候SGD就不太能满足要求了
- SGD容易收敛到局部最优,并且在某些情况下可能被困在鞍点【经查阅论文发现,其实在合适的初始化和step size的情况下,鞍点的影响并没这么大】
非自适应算法
动量SGD
SGD方法的一个缺点是,其更新方向完全依赖于当前的batch,因而其更新十分不稳定。解决这一问题的一个简单的做法便是引入momentum。
momentum即动量,它模拟的是物体运动时的惯性,即更新的时候在一定程度上保留之前更新的方向,同时利用当前batch的梯度微调最终的更新方向。这样一来,可以在一定程度上增加稳定性,从而学习地更快,并且还有一定摆脱局部最优的能力:
\begin{equation}
v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta)
\end{equation}
\begin{equation}
\theta = \theta - v_t
\end{equation}
其中,$\gamma$即momentum,表示要在多大程度上保留原来的更新方向,这个值在0-1之间,在训练开始时,由于梯度可能会很大,所以初始值一般选为0.5;当梯度不那么大时,改为0.9。$\eta$是学习率,即当前batch的梯度多大程度上影响最终更新方向,跟普通的SGD含义相同。$\gamma$ 与 $\eta$ 之和不一定为1。
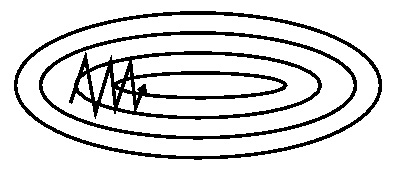
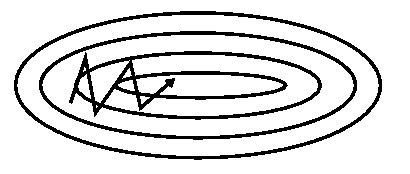
特点:
- 下降初期时,使用上一次参数更新,下降方向一致,乘上较大的$\gamma$能够进行很好的加速
- 下降中后期时,在局部最小值来回震荡的时候,$gradient\to0$,$\gamma$使得更新幅度增大,跳出陷阱
- 在梯度改变方向的时候,$\gamma$能够减少更新 总而言之,momentum项能够在相关方向加速SGD,抑制振荡,从而加快收敛
SGD has trouble navigating ravines, i.e. areas where the surface curves much more steeply in one dimension than in another, which are common around local optima. In these scenarios, SGD oscillates across the slopes of the ravine while only making hesitant progress along the bottom towards the local optimum as in Image 1.
Momentum is a method that helps accelerate SGD in the relevant direction and dampens oscillations as can be seen in Image 2. It does this by adding a fraction γ of the update vector of the past time step to the current update vector:
\begin{equation}
v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta)
\end{equation}
\begin{equation}
\theta = \theta - v_t
\end{equation}
Some implementations exchange the signs in the equations. The momentum term γ is usually set to 0.9 or a similar value.When cross-validated, this parameter is usually set to values such as [0.5, 0.9, 0.95, 0.99]. Similar to annealing schedules for learning rates (discussed later, below), optimization can sometimes benefit a little from momentum schedules, where the momentum is increased in later stages of learning. A typical setting is to start with momentum of about 0.5 and anneal it to 0.99 or so over multiple epochs.
Essentially, when using momentum, we push a ball down a hill. The ball accumulates momentum as it rolls downhill, becoming faster and faster on the way (until it reaches its terminal velocity if there is air resistance, i.e. γ<1).
The same thing happens to our parameter updates: The momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions. As a result, we gain faster convergence and reduced oscillation.
Nesterov Momentum
这是对传统momentum方法的一项改进,由Ilya Sutskever(2012 unpublished)在Nesterov工作的启发下提出的。
其基本思路如下图(转自Hinton的coursera公开课lecture 6a):
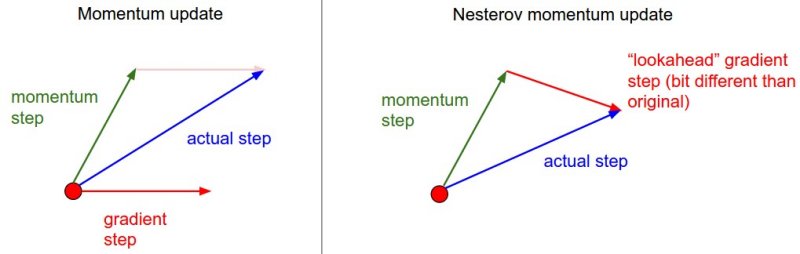
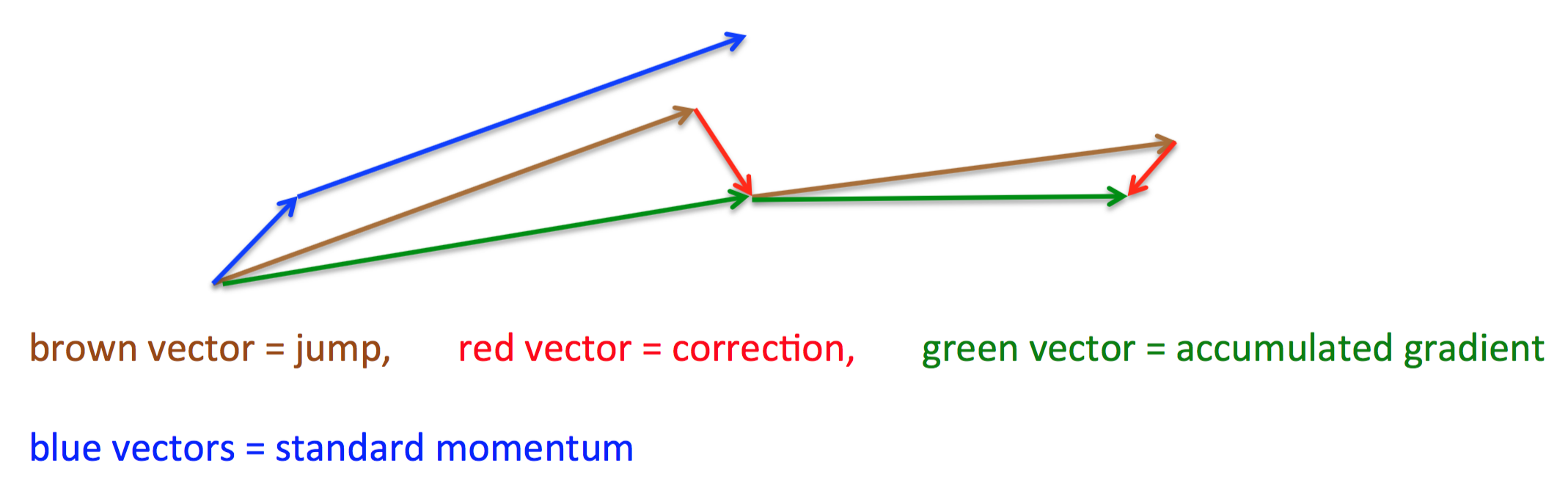
首先,按照原来的更新方向更新一步(棕色线),然后在该位置计算梯度值(红色线),然后用这个梯度值修正最终的更新方向(绿色线)。上图中描述了两步的更新示意图,其中蓝色线是标准momentum更新路径。
公式描述为:
\begin{equation}
v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta - \gamma v_{t-1} )
\end{equation}
\begin{equation}
\theta = \theta - v_t
\end{equation}
However, a ball that rolls down a hill, blindly following the slope, is highly unsatisfactory. We’d like to have a smarter ball, a ball that has a notion of where it is going so that it knows to slow down before the hill slopes up again.\\
Nesterov accelerated gradient (NAG) is a way to give our momentum term this kind of prescience. We know that we will use our momentum term γvt−1 to move the parameters θ. Computing $\theta−\gamma v_t−1$ thus gives us an approximation of the next position of the parameters (the gradient is missing for the full update), a rough idea where our parameters are going to be. We can now effectively look ahead by calculating the gradient not w.r.t. to our current parameters θθ but w.r.t. the approximate future position of our parameters:
Like momentum,NAG is a first-order optimization method with better convergence rate guarantee than gradient descent in certain situations. In particular, for general smooth(non-strongly) convex functions and a deterministic gradient, NAG achieves a global convergence rate of O($1/T^2$) (versus the O(1/T) of gradient descent), with constant proportional to the Lipschitz coefficient of the derivative and the squared Euclidean distance to the solution. While NAG is not typically thought of as a type of momentum, it indeed turns out to be closely related to classical momentum, differing only in the precise update of the velocity vector v.
learing rate 选择
常数learning rate
折半下降
每若干轮降低下learning rate,如每5轮降低一半,或者每20轮降低0.1
Reduce the learning rate by some factor every few epochs. Typical values might be reducing the learning rate by a half every 5 epochs, or by 0.1 every 20 epochs. These numbers depend heavily on the type of problem and the model. One heuristic you may see in practice is to watch the validation error while training with a fixed learning rate, and reduce the learning rate by a constant (e.g. 0.5) whenever the validation error stops improving. \par
指数下降
\begin{equation}
\alpha = \frac{\alpha_0}{e^{kt}}
\end{equation}
其中是$k$超参数,$t$是迭代轮数
$\frac{1}{t}$下降
\begin{equation}
\alpha = \frac{\alpha_0}{1+kt}
\end{equation}
数学形式,$k$是超参数,$t$是迭代轮数。
自适应算法
Adagrad
上面提到的方法对于所有参数都使用了同一个更新速率。但是同一个更新速率不一定适合所有参数。比如有的参数可能已经到了仅需要微调的阶段,但又有些参数由于对应样本少等原因,还需要较大幅度的调动。
Adagrad就是针对这一问题提出的,自适应地为各个参数分配不同学习率的算法。其公式如下:
\begin{equation}
\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{G_{t} + \epsilon}} \odot g_{t}
\end{equation}
其中$G^{t}\in R^{d\times d}$是一个对角矩阵,其中
\begin{equation}
G_{i, i} = \sqrt{\sum_{T=1}^tg_{T,i}^2}
\end{equation}
而$\epsilon$是一个平滑系数,使得不会出现除零的现象,通常在$10^{-8}$量级。Adagrad的一个主要优势是考虑了不同参数可能处在更新的不同阶段,同时避免了调参的问题,通常可以取 $\eta$为0.01.
Adagrad的一个主要缺点在于其参数的平方和累加:因为随着训练轮数的增加,每一个累加项都是正数,这使得整体的学习速率最终会变得非常的小,最终模型会静止不动(可能尚未到达收敛点).
特点:
- 前期$g_t$较小的时候, regularizer较大,能够放大梯度
- 后期$g_t$较大的时候,regularizer较小,能够约束梯度
- 适合处理稀疏梯度
缺点:
- 由公式可以看出,仍依赖于人工设置一个全局学习率
- $\eta$设置过大的话,会使regularizer过于敏感,对梯度的调节太大
- 中后期,分母上梯度平方的累加将会越来越大,使$gradient\to0$,使得训练提前结束
Adadelta
Adagrad算法存在三个问题
1.其学习率是单调递减的,训练后期学习率非常小
2.其需要手工设置一个全局的初始学习率
3.更新时,左右两边的单位不同一
Adadelta针对上述三个问题提出了比较漂亮的解决方案。其公式如下:
\begin{equation}
E[g^2]_t = \gamma E[g^2]_{t-1} + (1 - \gamma) g^2_t
\end{equation}
\begin{equation}
E[\Delta \theta^2]_t = \gamma E[\Delta \theta^2]_{t-1} + (1 - \gamma) \Delta \theta^2_t
\end{equation}
\begin{equation}
RMS[\Delta \theta]_{t} = \sqrt{E[\Delta \theta^2]_t + \epsilon}\end{equation}
\begin{equation}
\Delta \theta_t = - \dfrac{RMS[\Delta \theta]_{t-1}}{RMS[g]_{t}} g_{t}
\end{equation}
\begin{equation}
\theta_{t+1} = \theta_t + \Delta \theta_t
\end{equation}
$\gamma$的值近似在0.9左右,同时$\epsilon$是一个平滑系数,使得不会出现除零的现象,通常在$10^{-8}$量级.
可以看到,如此一来adagrad中分子部分需要人工设置的初始学习率也消失了。
Experiment: neural network MINIST$ ADADELTA > ADAGRAD > MOMENTUM > SGD$
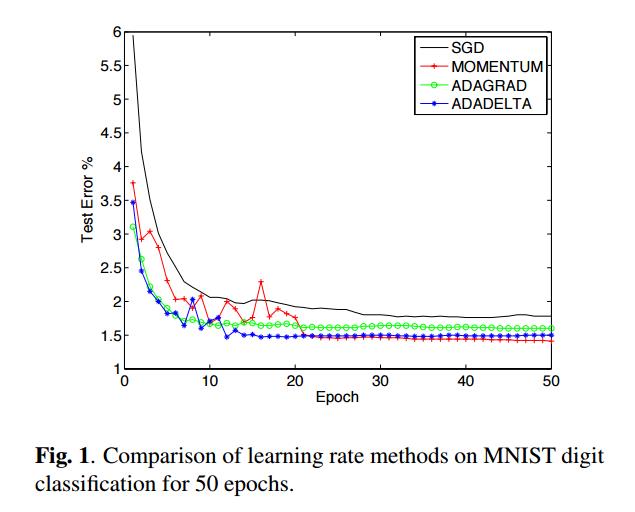
特点:
- 训练初中期,加速效果不错,很快
- 训练后期,反复在局部最小值附近抖动
RMSprop
RMSprop是一个未出版的,自适应学习速率方法,由Geoff Hinton提出。RMSprop和Adadelta的提出都源自于Adagrad,目的是为了解决Adagrad学习速率在迭代若干次后彻底消失的问题。本质上而言,其与Adadelta相同。
\begin{equation}
E[g^2]_t = 0.9 E[g^2]_{t-1} + 0.1 g^2_t
\end{equation}
\begin{equation}
\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}
\end{equation}
Hinton建议设置$\epsilon$为0.9,而$\eta$的学习速率为0.001.
特点:
- 其实RMSprop依然依赖于全局学习率
- RMSprop算是Adagrad的一种发展,和Adadelta的变体,效果趋于二者之间
- 适合处理非平稳目标 - 对于RNN效果很好
adam
\begin{equation}
m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t
\end{equation}
\begin{equation}
v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2
\end{equation}
\begin{equation}
\hat{m}_t = \dfrac{m_t}{1 - \beta^t_1}
\end{equation}
\begin{equation}
\hat{v}_t = \dfrac{v_t}{1 - \beta^t_2}
\end{equation}
\begin{equation}
\theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t
\end{equation}
该方法和RMSProp唯一的区别是smooth过程,这里使用的是m来做smooth操作,而不是使用原始的gradient vector. 论文中推荐的超参数为eps=1e-6, bata1=0.9, beta2=0.999, 在实践中, 如果没有其他的特殊理由,一般推荐使用Adam方法, 并且, Adam算法通常会比RMSProp算法效果好. 另外,也可以尝试SGD+Nesterov Momentum. 完整的Adam算法中还包括bias的纠正机制, 这事因为,在刚开始的几个steps中,m和v都要初始化, 并且在warm up 之前他们都biased at zero.
更多的细节可以参考论文原文.
特点:
- 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
- 对内存需求较小
- 为不同的参数计算不同的自适应学习率
- 也适用于大多非凸优化 - 适用于大数据集和高维空间
论文:The method computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients; the name Adam is derived from adaptive moment estimation. Our method is designed to combine the advantages of two recently popular methods: AdaGrad (Duchi et al., 2011), which works well with sparse gradients, and RMSProp (Tieleman & Hinton, 2012), which works well in on-line and non-stationary settings; important connections to these and other stochastic optimization methods are clarified in section 5.Some of Adam’s advantages are that the magnitudes of parameter updates are invariant to rescaling of the gradient, its stepsizes are approximately bounded by the stepsize hyperparameter, it does not require a stationary objective, it works with sparse gradients, and it naturally performs a form of step size annealing.
Adamax
- ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
Adamax是Adam的一种变体,此方法对学习率的上限提供了一个更简单的范围。公式上的变化如下:
\begin{equation}
m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t
\end{equation}
\begin{equation}
v_t = max(\beta_2 \times v_{t-1}, \left| g_t\right|)
\end{equation}
\begin{equation}
\hat{m}_t = \dfrac{m_t}{1 - \beta^t_1}
\end{equation}
\begin{equation}
\theta_{t+1} = \theta_{t} - \dfrac{\eta}{v_t + \epsilon} \hat{m}_t
\end{equation}
可以看出,Adamax学习率的边界范围更简单.
parameter: Keras recommend:
Good default settings for the tested machine learning problems are $\eta= 0.002$, $\beta_1 = 0.9$ and $\beta_2= 0.999$. With $\beta_1^t$ we denote $\beta_1$ to the power $t$. Here, $\frac{\eta}{1-\beta_1^t}$is the learning rate with the bias-correction term for the first moment.
Nadam
Nadam类似于带有Nesterov动量项的Adam。公式如下:
\begin{equation}
\hat{g_t}=\frac{g_t}{1-\Pi_{i=1}^t\beta_{1i}}
\end{equation}
\begin{equation}
m_t=\beta_{1t} \times m_{t-1}+(1-\beta_{1t})\times g_t
\end{equation}
\begin{equation}
\hat{m_t}=\frac{m_t}{1-\Pi_{i=1}^{t+1}\beta_{1i}}
\end{equation}
\begin{equation}
n_t=\beta_2\times n_{t-1}+(1-\beta_2)\times g_t^2
\end{equation}
\begin{equation}
\bar{m_t}=(1-\beta_{1t})\times \hat{g_t}+\beta_{1(t+1)}\times \hat{m_t}
\end{equation}
\begin{equation}
\hat{n_t}=\frac{n_t}{1-\beta_{2}^t}
\end{equation}
\begin{equation}
\Delta{\theta_t}=-\eta*\frac{\bar{m_t}}{\sqrt{\hat{n_t}}+\epsilon}
\end{equation}
可以看出,Nadam对学习率有了更强的约束,同时对梯度的更新也有更直接的影响。一般而言,在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果。
parameter: Keras recommend: lr=0.002, beta_1=0.9, beta_2=0.999, epsilon=1e-08, schedule_decay=0.004
All algorithms used $\beta_2$ = .999and $\epsilon$ = 1e−8 as suggested, with a momentum schedule given by $\beta_{1t} = \beta_1\times (1−0.5\times 0.96^{\frac{t}{250}})$ with $\beta_1$ = .99
对比
经验之谈
- 对于稀疏数据,尽量使用学习率可自适应的优化方法,不用手动调节,而且最好采用默认值
- SGD通常训练时间更长,但是在好的初始化和学习率调度方案的情况下,结果更可靠
- 如果在意更快的收敛,并且需要训练较深较复杂的网络时,推荐使用学习率自适应的优化方法。
- Adadelta,RMSprop,Adam是比较相近的算法,在相似的情况下表现差不多。
- 在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果
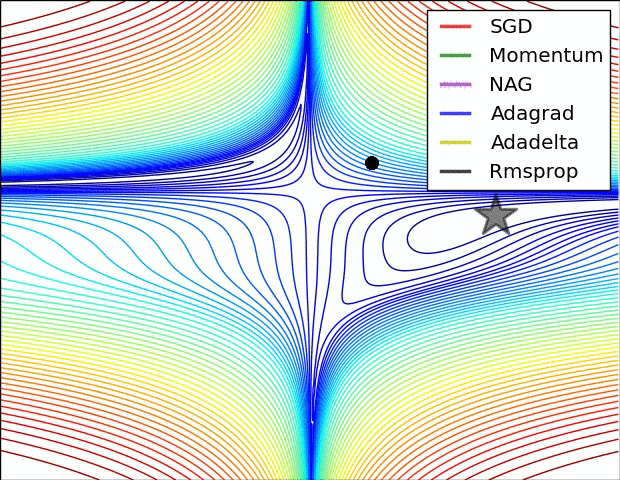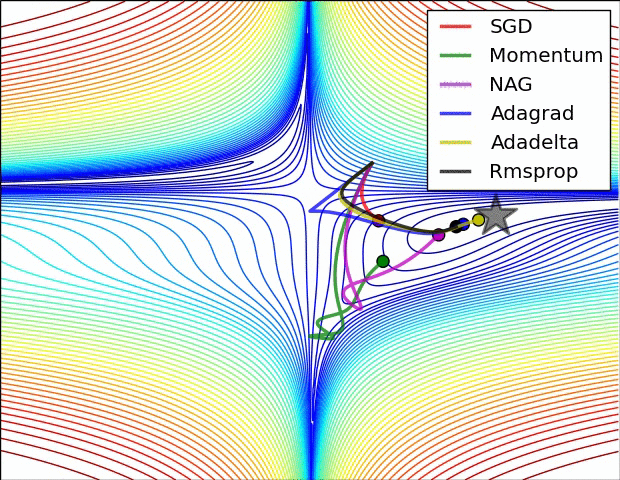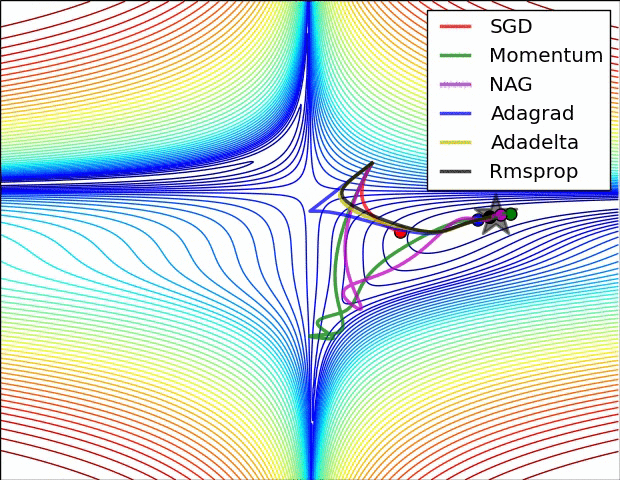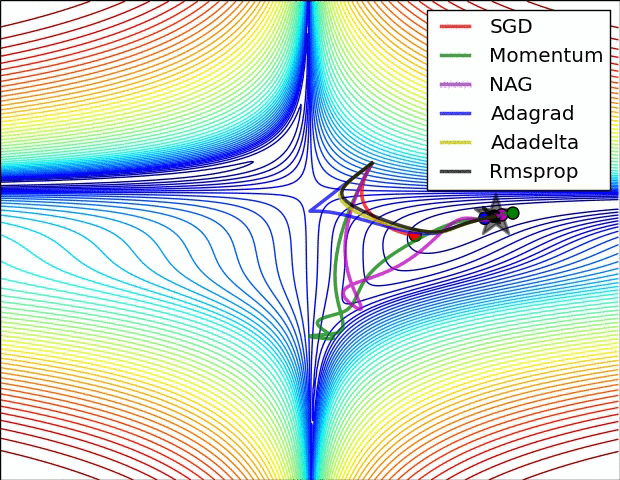
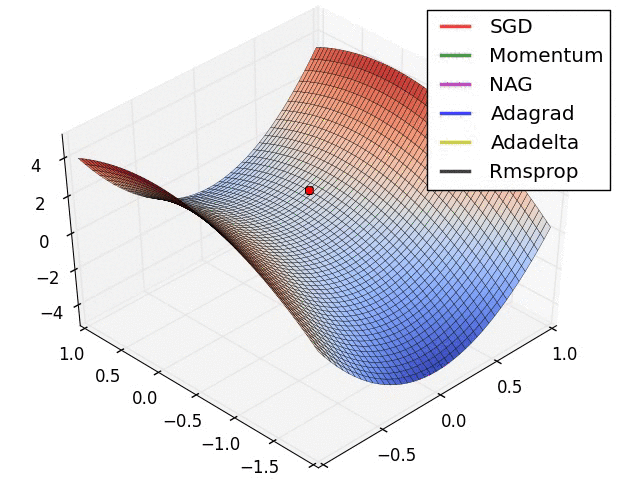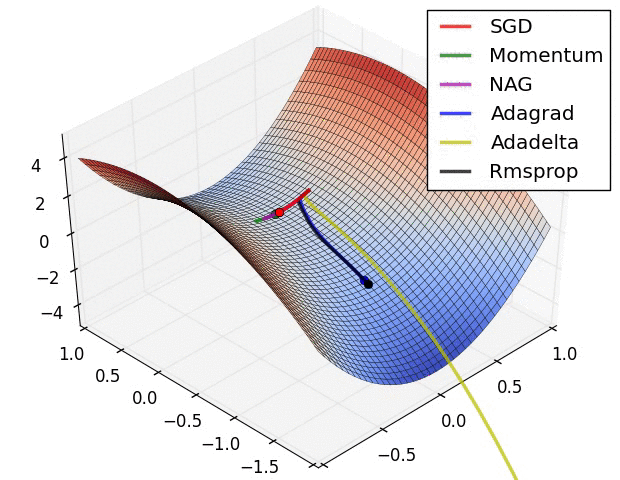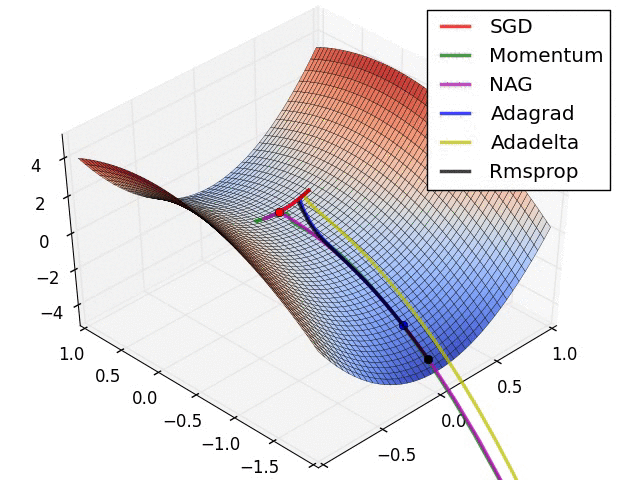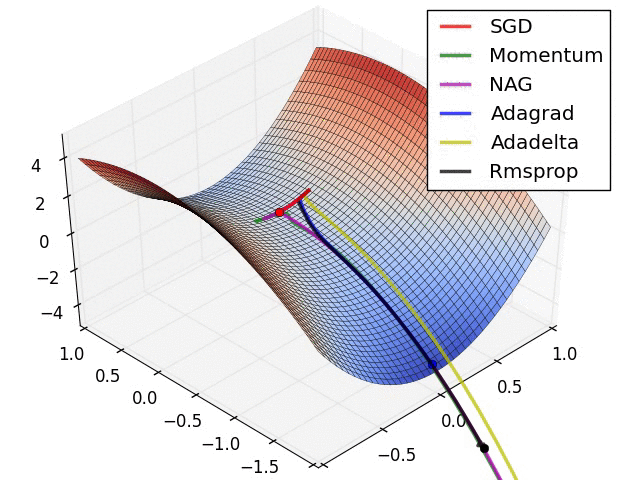
Experiment:
- MNIST Logistic regression
Adam> Nesterov > AdaGrad ( converage cost) - IMDB BoW feature logsitic regression
$ Adam \approx Adagrad \approx RMSProp \approx Nesterov$ - deepLearning
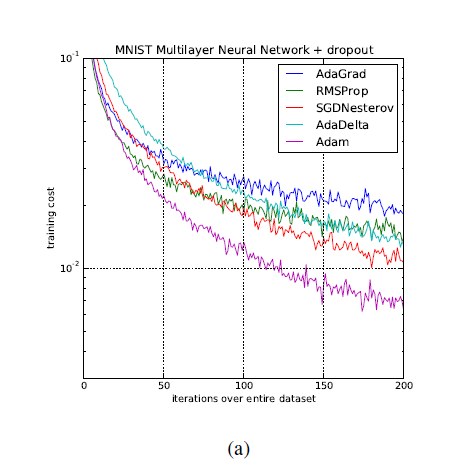
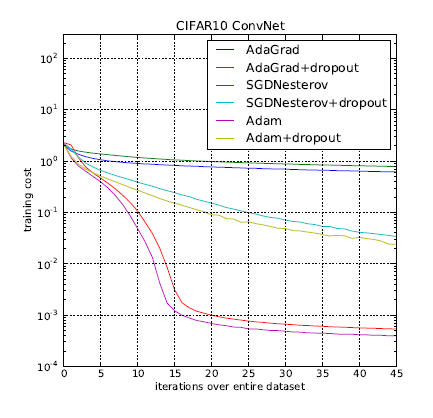
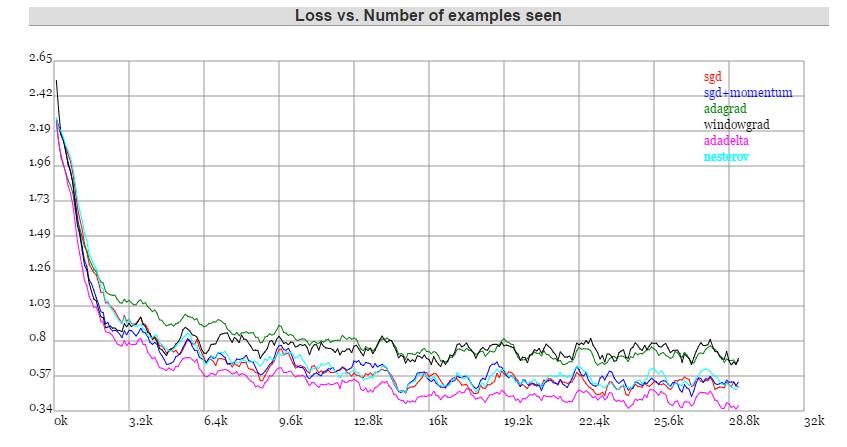
MINST: Adagrad/Adadelta并不需要设置学习速率,相对安全,但调好参数的SGD+动量表现也非常出色。
原文:This demo lets you evaluate multiple trainers against each other on MNIST. By default I’ve set up a little benchmark that puts SGD/SGD with momentum/Adagrad/Adadelta/Nesterov against each other. For reference math and explanations on these refer to Matthew Zeiler’s Adadelta paper (Windowgrad is Idea #1 in the paper). In my own experience, Adagrad/Adadelta are “safer” because they don’t depend so strongly on setting of learning rates (with Adadelta being slightly better), but well-tuned SGD+Momentum almost always converges faster and at better final values.
参考
http://sebastianruder.com/optimizing-gradient-descent/
https://zhuanlan.zhihu.com/p/22252270
https://keras.io/optimizers/
http://cs231n.github.io/neural-networks-3/#sgd
https://en.wikipedia.org/wiki/Stochastic_gradient_descent
http://blog.csdn.net/luo123n/article/details/48239963
http://blog.csdn.net/majordong100/article/details/51428642
http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
http://cs.stanford.edu/people/karpathy/convnetjs/demo/trainers.html
Paper
Unit Tests for Stochastic Optimization
ADADELTA: AN ADAPTIVE LEARNING RATE METHOD
ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION
Incorporating Nesterov Momentum into Adam