介绍
在数据挖掘中,经常会存在不平衡数据的分类问题,比如在异常监控预测中,由于异常就大多数情况下都不会出现,因此想要达到良好的识别效果普通的分类算法还远远不够,这里介绍几种处理不平衡数据的常用方法及对比。
记多数类的样本集合为L,少数类的样本集合为S。
用r=|S|/|L|表示少数类与多数类的比例。
基准
我们先用一个逻辑斯谛回归作为该实验的基准:
Weighted loss function
一个处理非平衡数据常用的方法就是设置损失函数的权重,使得少数类判别错误的损失大于多数类判别错误的损失。在python的scikit-learn中我们可以使用class_weight参数来设置权重。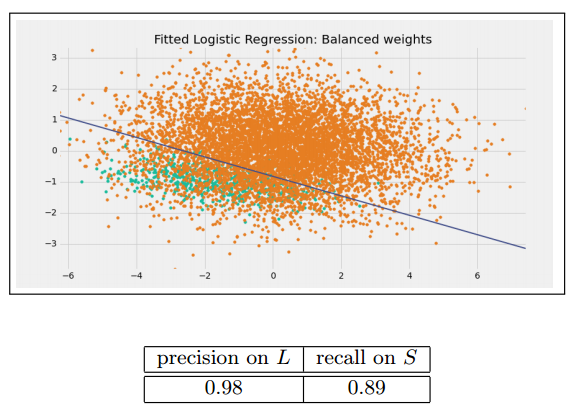
欠采样方法(undersampling)
Random undersampling of majority class
一个最简单的方法就是从多数类中随机抽取样本从而减少多数类样本的数量,使数据达到平衡。
但对于欠抽样算法,将多数类样本删除有可能会导致分类器丢失有关多数类的重要信息。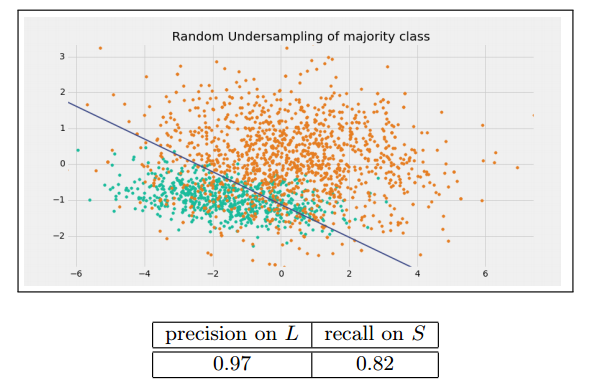
Edited Nearest Neighbor (ENN)
我们将那些L类的样本,如果他的大部分k近邻样本都跟他自己本身的类别不一样,我们就将他删除。
缺点:因为大多数的多数类样本的样本附近都是多数类,所以该方法所能删除的多数类样本十分有限。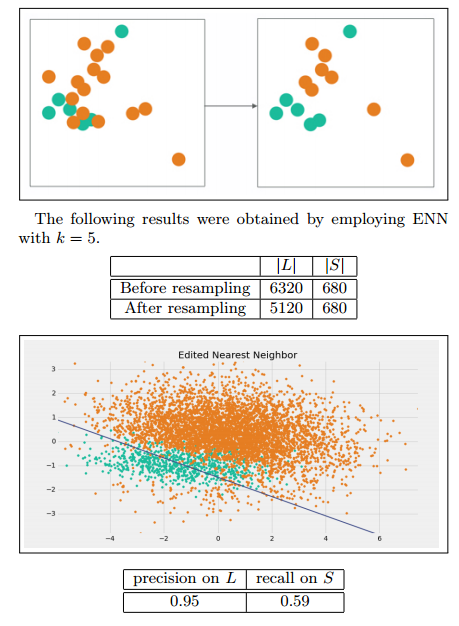
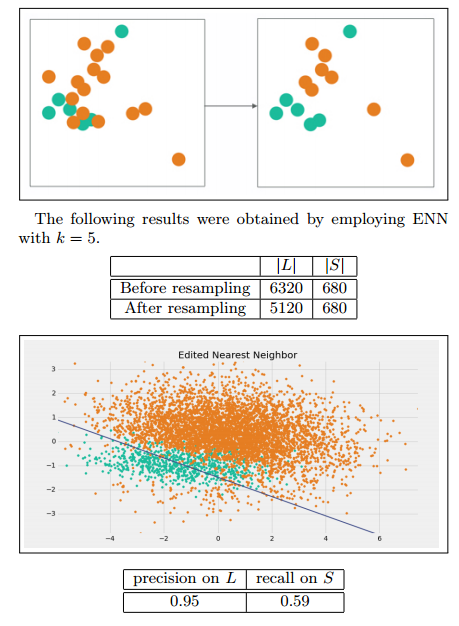
Repeated Edited Nearest Neighbor
这个方法就是不断的重复上述的删除过程,直到无法再删除为止。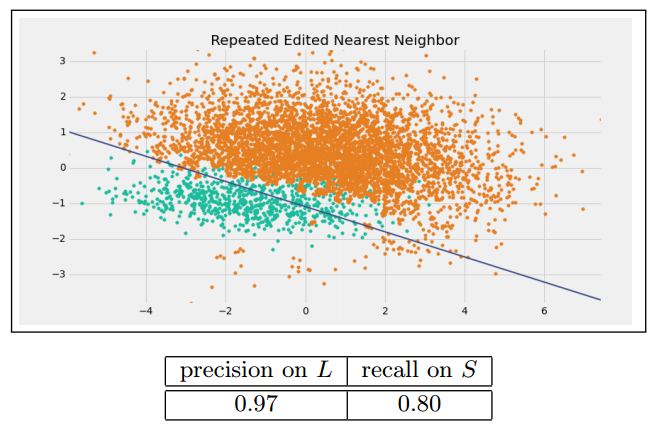
Tomek Link Removal
如果有两个不同类别的样本,它们的最近邻都是对方,也就是A的最近邻是B,B的最近邻是A,那么A,B就是Tomek link。我们要做的就是讲所有Tomek link都删除掉。那么一个删除Tomek link的方法就是,将组成Tomek link的两个样本,如果有一个属于多数类样本,就将该多数类样本删除掉。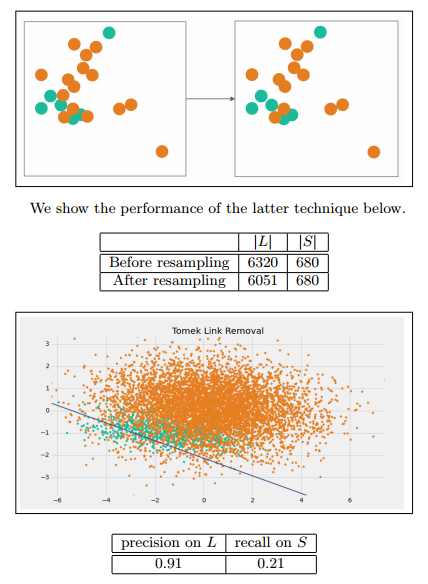
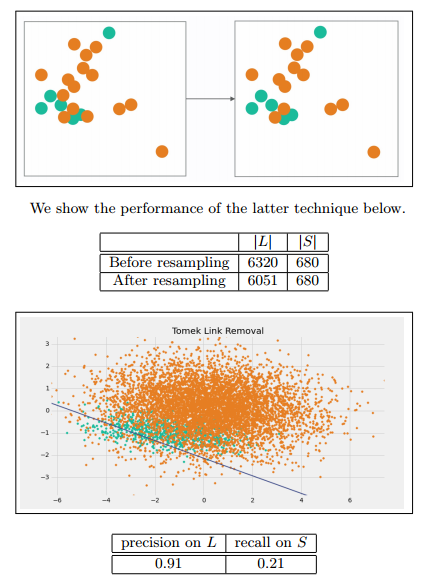
过采样方法(Oversampling)
我们可以通过欠抽样来减少多数类样本的数量从而达到平衡的目的,同样我们也可以通过,过抽样来增加少数类样本的数量,从而达到平衡的目的。
Random oversampling of minority class
一个最简单的方法,就是通过有放回的抽样,不断的从少数类的抽取样本,不过要注意的是这个方法很容易会导致过拟合。我们通过调整抽样的数量可以控制使得r=0.5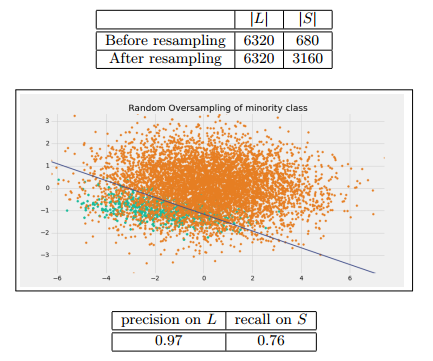
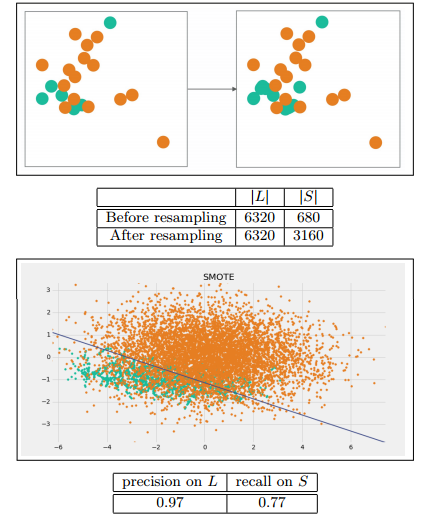
Synthetic Minority Oversampling Technique(SMOTE)
利用少数类样本控制人工样本的生成与分布,实现数据集均衡的目的,而且该方法可以有效地解决由于决策区间较小导致的分类过拟合问题。
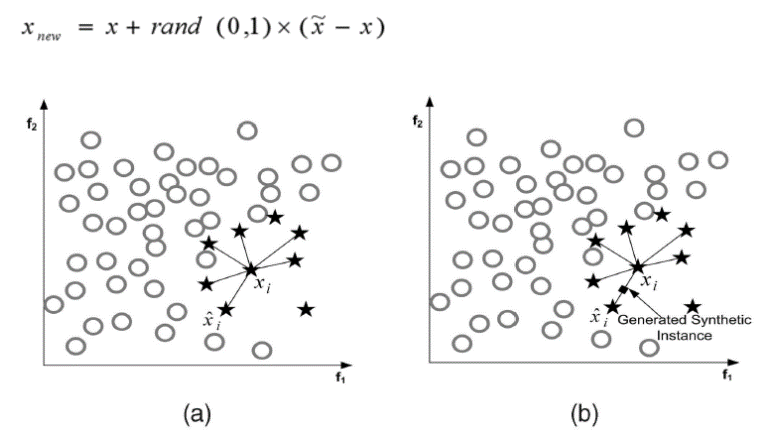
这是一个更为复杂的过抽样方法,他的方法步骤如下:
缺点
- Overgeneralization
- SMOTE’s procedure is inherently dangerous since it blindly generalizes the minority area without regard to the majority class.
- This strategy is particularly problematic in the case of highly skewed class distributions since, in such cases, the minority class is very sparse with respect to the majority class, thus resulting in a greater chance of class mixture.
- Lack of Flexibility
- The number of synthetic samples generated by SMOTE is fixed in advance, thus not allowing for any flexibility in the re-balancing rate.
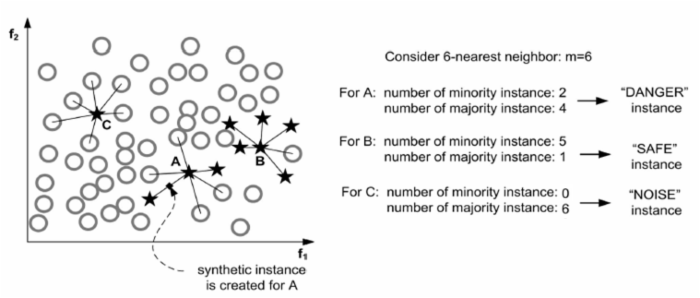
Borderline-SMOTE1
这里介绍两种方法来提升SMOTE的方法。
Borderline-SMOTE2
这个与Borderline-SMOTE1很像,只有最后一步不一样。
在DANGER集中的点不仅从S集中求最近邻并生成新的少数类点,而且在L集中求最近邻,并生成新的少数类点,这会使得少数类的点更加接近其真实值。
为了达到r=0.5 实验取k=5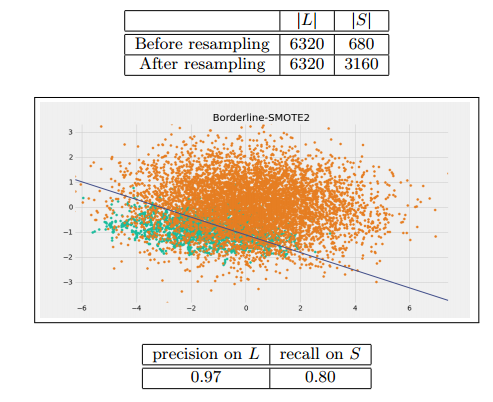
集成方法(Ensemble)
EasyEnsemble
一个最简单的集成方法就是不断从多数类中抽取样本,使得每个模型的多数类样本数量和少数类样本数量都相同,最后将这些模型集成起来。
算法伪代码如下:
- For i = 1, …, N:
(a) 随机从 L中抽取样本Li使得|Li| = |S|.
(b) 使用Li和S数据集,训练AdaBoost分类器Fi。
$$F_i(x)=sgn(\sum_{j=1}^nw_{ij}f_{ij}(x)-b_i)$$ - 将上述分类器联合起来
$$F(x)=sgn(\sum_{j=1}^nw_{ij}f_{i}(x))$$
BalanceCascade
这个方法跟EasyEnsemble有点像,但不同的是,每次训练adaboost后都会扔掉已被正确分类的样本,经过不断地扔掉样本后,数据就会逐渐平衡。

Reference: