本文是LDA算法的基本介绍。

维数约减 (Dimensionality Reduction)是把高维度数据在损失最小的情况下转换为低维度数据的动作。

动机：为什么需要维数约减

动机一：数据压缩

维数约减即减少数据的维度，比如从 2 维降成 1 维，从 3 维降成 2 维等。好处是节省内存，提高运算速度。比如，我们有多个特征，其中两个特征的相关性非常大，一个是用 cm 测量的长度，另外一个是用 inch 测量的长度 (实际上这可能是个真实的例子，因为一个实际问题可能有 1000 个特征，而采集这些特征的工程师可能不是同一个人，这样他们采集回来的数据就可能存在重复，即高相关性)。那么我们可以把这两个高相关性的特征用一条直线来表示，$x^{(i)} = {x_1^{(i)}, x_2^{(i)}}$ 简化为 $z^{(i)} = {z_1^{(i)}}$。相同的原理，如果在一个 3 维空间里，一些点基本分布在一个平面上，那么就可以把 3 维降成 2 维，即 $x^{(i)} = {x_1^{(i)}, x_2^{(i)}, x_3^{(i)}}$ 简化为 $z^{(i)} = {z_1^{(i)}, z_2^{(i)}}$。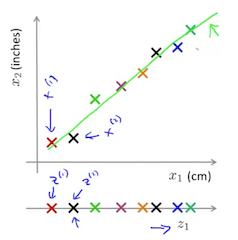

上图示例的就是把用英寸测量的特征和用厘米测量的特征合并起来的示意图。这里有个问题，为什么按 inch 测量的特征和按 cm 测量的特征不是在同一条直线上，而是在一条直线周围波动？实际上这个是正常的，因为测量的人和误差等方面的原因，会导致特征采集时数据会在误差范围内波动。

动机二：数据可视化

比如考查一个国家的经济状况，可能会有 50 个特征，经济总量，人均 GDP，出口值，进口值等等。如果想要直观地观察多个特征之间的关系，就比较难办。因为我们很难画出 50 个特征的图出来。这个时候，我们可以把 50 个特征简化为 2 维或 3 维的数据，然后画出 2D 或 3D 图出来，就可以直观地观察这些数据的样子。

主成份分析法

主成份分析法简称 PCA (Principal Component Analysis)，这是目前最常用和流行的数据降维方法。

假设需要把 2 维数据降为 1 维数据时，我们需要找出一个向量 $u^{(1)}$ ，以便让 2 维数据的点在这个向量所在的直线上的投射误差最小。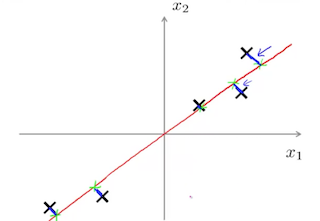

上图中，我们的目标就是找到红色的向量所在的直线，以便让所有黑色的点到这条直线的平均距离最短，这样我们就可以把原来在二维平面上的点映射到在红色直线所在的一维直线上的绿色的点来表示。即把二维数据降为一维数据。

假如需要把 3 维数据降为 2 维数据时，我们需要找出两个向量 $u^{(1)}, u^{(2)}$，以便让 3 维数据的点在这两个向量所决定的平面上的投射误差最小。

从数学角度更一般地描述 PCA 算法，当我们需要从 n 维数据降为 k 维数据时，我们需要找出 k 个向量 $u^{(1)}, u^{(2)}, … , u^{(k)}$ ，把 n 维的数据投射到这 k 个向量决定的线性空间里，最终使投射误差最小化的过程。

PCA 算法主要步骤

步骤一：数据归一化和缩放

在进行 PCA 算法前，需要对数据进行预处理。预处理包括两个步骤：

数据归一化 (Mean Normalization)：使数据的均值为零。加快 PCA 运算速度。
数据缩放 (Feature Scaling)：使不同的特征数值在同一个数量级。

数据归一化公式为：
$$
z_j^{(i)} = x_j^{(i)} - \mu_j
$$
其中，$\mu_j$ 是训练样本中第 j 个特征 ($x_j^{(i)}$) 的平均值。然后用 $z_j^{(i)}$ 代替 $x_j^{(i)}$ 进行 PCA 运算。
接着对数据进行缩放，缩放只在不同特征数据不在同一个数量级上时才使用。
$$
x_j^{(i)} = \frac{x_j^{(i)} - \mu_j}{s_j}
$$
其中，$\mu_j$ 是训练样本中第 j 个特征 ($x_j^{(i)}$) 的平均值
$$
\mu_j = \frac{1}{m} \sum_{i=1}^m x_j^{(i)}
$$
$s_j$ 是训练样本中第 j 个特征 ($x_j^{(i)}$) 的范围，即 $s_j = max(x_j^{(i)}) - min(x_j^{(i)})$。

步骤二：计算协方差矩阵的特征向量

数据预处理完，我们需要计算协方差矩阵 (Covariance Matrix)，用大写的 Sigma 表示 (大写的 Sigma 和累加运算符看起来几乎一样，但这里其实是一个数学符号而已，不是累加运算)：
$$
\Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)}) (x^{(i)})^T
$$
如果把训练样例用行向量来表示，那么 X 将是一个 m x n 的矩阵，m 是训练样例个数，n 是特征个数。向量化计算 Sigma 的公式将是：
$$
\Sigma = \frac{1}{m} X^T X
$$
计算结果 Sigma 将是一个 n x n 矩阵。接着，计算协方差矩阵的特征向量 (eigenvectors)：
$$
[U, S, V] = svd(Sigma)
$$
svd 是奇异值分解 (Singular Value Decomposition)，是高级线性代数的内容。在 Octave 里，也可以使用 eig 函数来求解协方差矩阵的特征向量。这里，Sigma 是 n x n 矩阵，经过 svd 运算后，我们真正关心的是 U。它是一个 n x n 矩阵。如果我们选择 U 的列作为向量，那么我们得到 n 个列向量 $u^{(1)}, u^{(2)}, … , u^{(n)}$，我们如果需要把数据降维为 k 维，那么我们只需要选取前 k 个向量即可，即 $u^{(1)}, u^{(2)}, … , u^{(k)}$。

步骤三：数据降维

接着，我们计算降维后的值 z，假设降维前的值为 $x^{(i)}$，降维后为 $z^{(i)}$，那么：

$$
z^{(i)} = U_{reduce}^T x^{(i)}
$$

其中，$U_{reduce} = [u^{(1)} u^{(2)} … u^{(k)}]$。看一下数据维度，$U_{reduce}$ 是 n x k 矩阵，$x^{(i)}$ 是 n x 1 矩阵，$z^{(i)}$ 是 k x 1 矩阵。

实现时可以用向量化来提高性能。假设 X 是 m x n 矩阵，m 表示训练样例个数，n 表示特征数。用大写的 Z 表示降维后的数据，是一个 m x k 的矩阵。$U_{reduce}$ 是 n x k 的主成份特征矩阵，每列表示一个主成份特征。那么他们满足下面的关系：

$$
Z = X * U_{reduce}
$$

要从数学上证明这样计算出来的 $z^{(i)}$ 就是 $x^{(i)}$ 在 $U_{reduce}$ 线性空间投射，使得其投射误差最小，将是一个非常复杂的过程。所幸如果我们单纯从应用 PCA 算法来对数据进行降维的角度来看的话，借用 Octave/Matlab 等现成函数，计算过程相对比较简单。

PCA 的应用

数据还原

我们怎么样从压缩过的数据里还原出压缩前的数据呢？从前文的计算公式，我们知道降维后的数据计算公式 $z^{(i)} = U_{reduce}^T x^{(i)}$。所以，如果要还原数据，我们可以使用下面的公式：

$$
x_{approx}^{(i)} = U_{reduce} z^{(i)}
$$

其中，$U_{reduce}$ 是 n x k 维矩阵，$z^{(i)}$ 是 k x 1 列向量。这样算出来的 $x^{(i)}$ 就是 n x 1 列向量。

向量化运算公式为：

$$
X_{approx} = Z * U_{reduce}^T
$$

其中 $X_{approx}$ 是还原回来的数据，是个 m x n 矩阵，每行表示一个训练样例。Z 是个 m x k 矩阵，是压缩后的数据。$U_{reduce}$ 是 n x k 的主成份特征矩阵，每列表示一个主成份特征。

PCA 算法中 K 参数的选择

怎么样选择参数 K 呢？K 是主成份分析法中主成份的个数。可以用下面的公式来判断选择的 K 是否合适：

$$
\frac{ \frac{1}{m} \sum_{i-1}^m | x^{(i)} - x_{approx}^{(i)} |^2 }{ \frac{1}{m} \sum_{i=1}^m | x^{(i)} | } \le 0.01
$$

其中分子部分表示平均投射误差的平方；分母部分表示所有训练样例到原点的距离的平均值。这里的物理意义用术语可以描述为 99% 的数据真实性被保留下来了 (99% of variance is retianed)。简单地理解为压缩后的数据还原出原数据的的准确度为 99%。另外常用的比率还有 0.05 ，这个时候准确度就是 95%。在实际应用中，可以根据要解决的问题的场景来决定这个比率。

假设我们的还原率要求是 99%，那么用下面的算法来选择参数 K：

让 K = 1
运行 PCA 算法，计算出 $U_{reduce}, z^{(1)}, z^{(2)}, … , z^{(m)}, x_{approx}^{(1)}, x_{approx}^{(2)}, … , x_{approx}^{(m)}$
利用 $\frac{ \frac{1}{m} \sum_{i-1}^m | x^{(i)} - x_{approx}^{(i)} |^2 }{ \frac{1}{m} \sum_{i=1}^m | x^{(i)} | }$ 计算投射误差率，并判断是否满足要求，如果不满足要求，K = K + 1，继续步骤 2；如果满足要求，K 即是我们选择的参数

这个算法容易理解，但实际上效率非常低下，因为每做一次循环都需要运行一遍 PCA 算法。另外一个更高效的方法是利用 svd 函数返回的 S 矩阵：$[U, S, V] = svd(Sigma)$。其中 S 是个 n x n 对角矩阵，即只有对角线上的值非零其他元素均为零。

从数学上可以证明（从应用角度，可以忽略这个证明过程），投射误差率也可以使用下面的公式计算：

$$
1 - \frac{\sum_{i=1}^k S_{ii}}{\sum_{i=1}^n S_{ii}}
$$

这样运算效率大大提高，我们只需要调用一次 svd 函数即可。

加快监督机器学习算法的运算速度

PCA 的一个典型应用是用来加快监督学习 (Supervised Learning) 的速度。

比如，我们有 m 个训练数据 $(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), … , (x^{(m)}, y^{(m)})$，其中 $x^{(1)}$ 是 10,000 维的数据，想像一下，如果这是个图片分类问题，如果输入的图片是 100 x 100 分辨率的。那么我们就有 10,000 维的输入数据。

使用 PCA 来加快算法运算速度时，我们把输入数据分解出来 $x^{(1)}, x^{(2)}, … , x^{(m)}$，然后运用 PCA 算法对输入数据进行降维压缩，得到降维后的数据 $z^{(1)}, z^{(2)}, … , z^{(m)}$，最后得到新的训练样例 $(z^{(1)}, y^{(1)}), (z^{(2)}, y^{(2)}), … , (z^{(m)}, y^{(m)})$。利用新的训练样例训练出关于压缩后的变量 $z$ 的预测函数 $h_\theta(z)$。

需要注意，PCA 算法只用来处理训练样例，运行 PCA 算法得到的转换参数 $U_{reduce}$ 可以用来对交叉验证数据集 $x_{cv}^{(i)}$ 以及测试数据集 $x_{test}^{(i)}$ 进行转换。当然，还需要相应地对数据进行归一化处理或对数据进行缩放。

PCA 误用

PCA 的典型应用场景是对数据进行压缩，减少磁盘/内存占用，加快算法运行速度。另外一个是用来数据可视化 (降到 2 维或 3 维)。我们了解到 PCA 可以对数据进行降维，即减少特征数，有人用 PCA 来解决过拟合问题。这可能在某些情况下会起作用，但实际上 PCA 不是一个好的解决过拟合的方法。解决过拟合应该使用正则化，加大成本函数里正则项的比重。

PCA 滥用

另外一个场景是在设计机器学习算法时，一开始就引入 PCA 来对数据进行压缩降维。实际上这不是好的方法。我们应该尽量使用原始数据来进行机器学习运算，当出现问题时，比如内存占用太大，运算时间太长等问题时，我们才考虑用 PCA 来优化。PCA 是算法优化的一个步骤，而不是机器学习系统里的必须步骤。

参考：