Downpour SGD(大规模分布式深度网络)

发表于   |   分类于   |  

Parallel SGD Paper
Large Scale Distributed Deep Networks

摘要

最近关于无监督特征学习（unsupervised feature learning）和深度学习（deep learning）的工作表明，具有训练大型模型能力的系统能够显著地提升深度神经网络的训练效果。在这篇文章中，我们针对的问题是利用多达10^4数量的CPU来训练一个具有10^9数量的参数（parameter）的深度网络。为了达到训练的目的，我们开发了称为DistBelief的软件框架，其利用具有上千节点（译者注：为了一致性，译文中的节点均指机器，即计算节点；而神经网络中的节点，均称为单元）的计算集群来训练大型模型。

在该框架中，实现了两个算法用于大规模分布训练：

  1. Downpour（译者注：猜测这里的Downpour主要是指并行地参数更新，就像倾盆大雨中，雨点从多处同时落下一样）SGD（stochastic gradient descent），一个支持大量模型副本的异步随机梯度下降过程。
  2. Sandblaster（译者注：形容来自coordinator的命令像砂粒一样喷向集群其他节点），一个支持多种批量（batch）计算的分布优化方法，包含了L-BFGS的分布式实现，Downpour SGD和Sandblaster L-BFGS 都具有提升系统扩展能力和加速深度网络训练的能力。

我们已经成功地利用DistBelief训练出一个比先前研究中提到的大30余倍的深度网络模型，并且获得了针对ImageNet（一个具有21K个分类和10M图像视觉识别任务）的最先进的训练效果。同时，我们还证明了，以上提及的技术能够显著地提升一个中等大小的，用作商用语音识别服务的深度网络的训练效果。尽管我们的这些技术主要用在大型神经网络的训练上，但是相关的算法同样适用于任何基于梯度的机器学习算法。

介绍

深度学习和无监督特征学习给许多实际应用带了新的巨大希望。它在包括语音识别[1, 2]、视觉物体识别[3, 4]和文本处理[5, 6]等不同领域上体现了最领先的性能优势和效果。 先前研究已经证明，通过增加样本数量和模型参数数量等不同手段，可以显著地提升分类算法的最终精确度[3, 4, 7]。该结论掀起了研究可扩展的深度学习训练和推断算法和提高其适用性等优化方法的热潮[7, 9]。近年来，在中等大小深度网络的训练上，一个重要的进步是因GPU的使用，使其变得更加的实用[1, 2, 3, 8]。但GPU众所周知的缺陷是，当其内存（通常小于6G）无法存放下模型时，训练的提升效果变得不再明显。这时，为了有效地使用GPU，研究者往往通过减少样本或变量规模的途径使得CPU和GPU之间的数据交换不在成为瓶颈。虽然数据或变量的减少对小规模问题（如针对于声学模型的语音识别）有效，但对具有大量样本和高维度变量的问题（如高分辨率图像）将失去效果。
在本文中，我们提出了一个替代的方法，使用大规模的计算集群来分布地对深度网络进行训练和推断。我们开发了一个既能提升节点内（通过多线程方式）又可提升节点间（通过消息传递）并行训练能力的软件框架，称为DistBelief。它管理了如并行计算、同步化和通信等底层的细节。除了支持模型并行，DistBelief同时还支持数据并行，通过单一模型的多个分布副本的方式来优化同一目标。在该框架中，我们设计并实现了两个用于大规模分布式训练的新方法：i)Downpuur SGD，一个利用自适应学习速率和支持大量模型副本的异步随机梯度下降过程；(ii)Sandblaster L-BFGS，L-BFGS过程的一个分布式实现，其利用了数据和模型的并行（原作者注：我们利用Sandblaster方法实现了L-BFGS，但是Sandblaster同样广泛适用于其他批量方法的优化）。两个方法相比较于常规的SGD或L-BFGS方法都获得了显著的速度提升。 关于大规模非凸方法优化，我们的实验呈现了一些出人意料的结果。首先，异步梯度下降，一个很少被用到非凸问题的方法，尤其是与Adagrad[10]自适应学习速率结合时，用以训练深度网络的效果很好。其次，当计算资源充足时，L-BFGS方法能够和许多SGD的变种方法相匹敌，甚至优于后者。 对于深度学习的特定应用，我们提出了两项发现：前面提及的分布式优化方法，不仅可以加速中等规模模型的训练，同时它也可以训练规模大于想象的模型。为了证明第一点，我们利用分布式集群来训练中等大小语音识别模型，获得了与GPU相同的分类精度，而耗时仅是后者的1/10。为了证明第二点，我们训练了一个具有1G数量参数的大型神经网络，并用训练结果把ImageNet（计算机视觉领域最大的数据库之一）判别分类结果提升到了最先进的水平。

前期工作

近年来，用于商业和学术的机器学习数据集呈空前增长的趋势。因此，一些研究者开始探索可扩展的机器学习算法来处理这些泛洪数据[11, 12, 13, 14, 15, 16, 17]。但大量的研究仍着眼于线性凸模型[11, 12, 17]。在凸模型中，分布式梯度计算自然是第一步，但是有时因为同步的问题会遭遇训练速度减慢。针对该问题，已经有一些有效果的工作，如异步随机梯度下降算法中的无锁参数更新（如Hogwild![19]）。不幸的是，将这些方法扩展到的非凸情况的研究，如处理训练深度网络中遇到的问题，还是一片未知的领域。特别地，在存在多个局部最小解的情况下，是否能够使用参数平均或者执行密集的异步参数更新方法，还是未知的问题。 在深度学习范畴中，大多数工作仍然集中在利用单节点训练较小规模模型（如Theano[20]）上。关于向上扩展深度学习的一些有意思的建议是，利用GPU来训练多个小型模型，然后将分别的预测结果取平均[21]，或者修改标准的深度网络使其能够从本质上并行化。而与这些前期工作不同，我们关注于扩展深度网络用于训练具有10^9参数数量的超大模型，同时避免给模型形式引入限制。在分布式扩展方面，模型的并行，其思想和[23]类似，是一个主要的组成部分，同时其也必须和巧妙的分布优化方法相结合以利用数据的并行性。 我们也考虑了用一些现有的大规模计算工具，如Mapreduce和GraphLab等来处理大规模深度学习。我们发现为数据并行处理而设计的Mapreduce，极其不适合深度网络训练中固有的迭代计算；而用于通用（通常是无结构的）图计算的GraphLab，同样没有利用模型并行深度网络中典型的分层图结构来提升计算效率。

模型并行

为了使超大规模深度网络的训练变得容易，我们开发了软件框架——DistBelief，用以支持神经网络的并行计算和分层图形模型。用户只需定义发生在每个单元上的计算过程以单元在向上传递和向下传递（原作者注：对于神经网络而言，“向上”和“向下”指的是“前馈”和“反向传播”，而对于隐式Markov模型，它们与“前向”和“后向”意思更相近）时需发送的消息。对于大型模型，用户可能会将模型加以划分（如图1所示），使得不同节点的计算任务被分配到了不同机器上。DistBelief自动地利用CPU资源将节点内计算并行化，同时它还管理了底层通信、同步化和在训练和推断时的机器间数据传输。 将深度网络分布到多个机器上所带来的性能提升主要取决于模型的连通结构和计算需求。具有大量参数或高计算需求的模型通过增加CPU和内存数量通常可以提升训练速度，直到增加到通信开销成为系统的瓶颈。我们已成功地在144个划分（机器）上运行DistBelief框架，且获得了显著的性能提升，同时在8或16个划分上运行的一个中等大小模型，也获得了很好的效果（请参考第5节中模型并行化基准测试中的实验结果）。显然地，局部连通的网络模型，因为需要更少的网络通信，所以比全连通网络模型更易于分布化。导致性能退化的一个主要原因是因不同机器上处理时间的不同，导致大量的机器在等待一个或单个节点完成本阶段任务（译者注：和MapReduce中Map阶段的长尾问题类似）。尽管如此，对于我们最大的模型来讲，我们仍可以高效地用总共有512核CPU 的32台机器（每台机器平均使用16核CPU的计算资源）来训练单个神经网络。当和下一节中讲到的利用模型多副本方法的分布式优化算法相结合时，将使得在多达10K的CPU数量上训练单个网络成为可能，从而进一步减少总的训练时间。

分布式优化算法

DistBelief框架中的并行计算方法使我们能够部署和运行比前期工作中提到的大得多的神经网络模型。但是为了在合理时间内训练如此规模的模型，这就要求我们不仅需实现单个DistBelief实例内的并行，而且需要将训练任务分发到多个DistBelief实例。在本节中，我们将具体阐述这第二级的并行，即采用多个DistBelief模型的实例（或副本），同时来达到一个优化目标。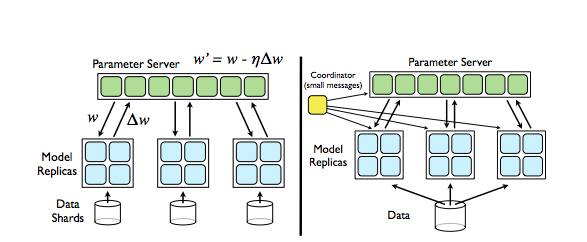
large_scale.png

  • 左：Downpour SGD，模型的副本采用异步方式从参数服务器（Parameter Server）中获取参数w和上传Δw到参数服务器。
  • 右：Sandblaster L-BFGS：单个协调器（Coordinator）实例发送简短消息（message）到模型副本和参数服务器以协调批量优化过程。

下面我们来对这两个分布优化方法做比较：Downpour SGD是在线方法，而L-BFGS是批量方法。两方法中模型副本都利用了中心分割化服务器组的概念来共享参数，也都利用了每个模型副本中DistBelief的并行性。但更重要的是，对不同副本的处理时间的不同，甚至整个模型副本的失效、移除和重启等情况都在两方法的考虑范围之内。

Downpour SGD

随机梯度下降（SGD）方法，应该是最常用的训练深度神经网络的优化方法[26, 27, 3]。但不幸的是，传统SGD方法本质上的顺序性，使得在大型数据集下变得不再适用，因为这种完全串行方式所需要的机器间数据移动是非常耗时的。

为了将SGD应用到大数据集上，我们提出了Downpour SGD，一个使用单个DistBelief模型的多个分布副本的异步随机梯度下降变种。它的基本方法如下：将训练集划分若干子集，并对每个子集运行一个单独的模型副本。模型副本之间的通信均通过中心参数服务器组，该参数服务器组维护了模型参数的当前状态，并分割到多台机器上（例如，如果我们参数服务器组有10个节点，那么每个节点将负责存储和更新模型参数的1/10，如图1所示）。该方法在两个方面体现异步性：

  1. 模型副本之间运行独立
  2. 参数服务器组各节点之间同样是独立的。

考虑Downpour SGD的一个最简单的实现，在处理每个mini-batch（译者注：小型批量）之前，模型副本都会向参数服务器请求最新的模型参数。因为DistBelief框架也是分布在多台机器上，所以其框架的每个节点只需和参数服务器组中包含和该节点有关的模型参数的那部分节点进行通信。在DistBelief副本获得更新后的模型参数后，运行一次mini-batch样本来计算参数的梯度，并推送到参数服务器，以用于更新当前的模型参数值。
可以通过设定每Nfetch 次mini-batch操作向参数服务器获取一次更新后的参数和每npush次mini-batch操作推送一次梯度更新到参数服务器（这里nfetch不一定和npush相等）。事实上，获取参数，推送梯度和处理训练样本三种操作，可以以三个采用弱同步的线程实现（参见附录中的伪代码）。为了简单起见，同时也是为了和传统SGD方法相比较，在下面的实验中，我们设定: Nfetch=Npush=1
在处理机器失效方面，Downpour SGD比标准（同步）SGD要鲁棒。对于同步SGD来讲，如果一台机器失效，整个训练过程将会延时；但是对于异步SGD来讲，如果某个模型副本的一台机器失效，其他模型副本仍然继续处理样本并更新参数服务器中的模型参数。另一方面，Downpour SGD带来的多种异步处理形式给优化过程带来了进一步的随机性。这里面最显而易见的是，模型实例最可能是使用一个稍微过时的参数来计算梯度，因为这时其他的副本可能已经更新了参数服务器上的参数。但是，除此之外还有其他随机的来源：因为参数服务器组的每台机器是行为独立的，所以无法保证在给定时间点上，每个节点的参数被更新的次数相同，或者以同样的顺序被更新。更进一步的，因为模型副本使用不同的线程来获取参数和推送梯度值，故在同一时间戳上，单个副本内的参数将有额外的稍微不一致的现象。尽管对于非凸问题的这些操作的安全性缺乏理论基础，但是在实践中，我们发现放松一致性要求的做法是相当有效的。

我们发现，另外一项能极大提高Downpour SGD鲁棒性的技术是使用Adagrad[10]自适应学习速率方法。与使用固定的值作为学习速率的方式不同，Adagrad的每个参数使用单独的自适应学习速率。
可以看出，因为学习速率的计算仅与参数历史梯度值的平方和有关，所以Adagrad易于在每个参数服务器节点上单独实现。所有学习速率共享的缩放常量因子γ，通常大于（可能有一个数量级）不使用Adagrad情况下，采用固定学习速率的最优值。Adagrad的使用能够增加并发训练的模型副本数量，同时，采用“热启动”（即在启动其他副本之前，用单个模型来训练参数）的模型训练方法，几乎消除了在Downpour SGD中可能会出现的稳定性问题.

假设$\eta_{i,k}$是第i个参数在第k次迭代时的学习速率,$\Delta g_{i,k}$是其梯度值,那么：
\begin{equation}
\eta_{i,k}=\frac{\gamma}{\sqrt{\sum^k_{j=1} g_{i,k}}}
\end{equation}
downpour.jpeg

Sandblaster L-BFGS

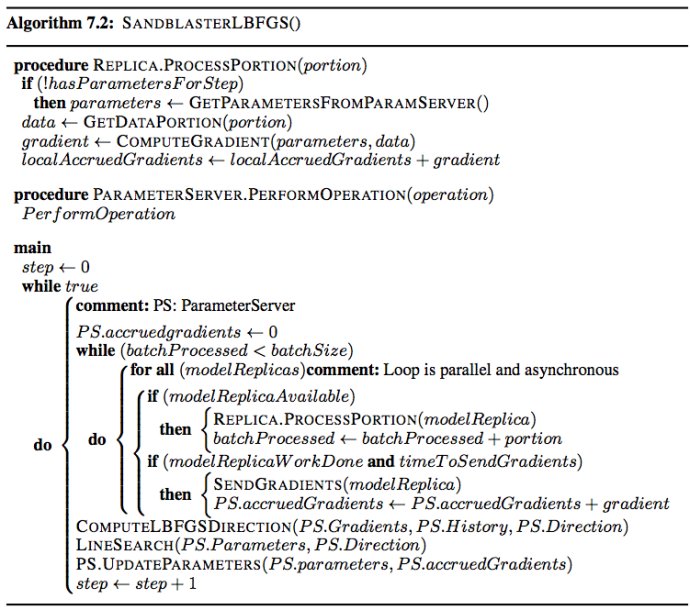
已经证实批量处方法在小型深度网络的训练上效果很好[7]。为了将这些方法运用到大型模型和大型数据集上，我们引入了Sandblaster批量优化框架，同时讨论了L-BFGS在该框架的一个实现。 Sandblaster的主要思路是将参数的存储和操作分布化，算法（如L-BFGS）的核心位于协调器（coordinator）中。该协调器并不直接获取模型参数，相反地，它发出一系列命令（如内积，向量缩放，系数相关加法，乘法）到参数服务器节点，并且这些命令能在节点范围内执行。一些额外的信息，如L-BFGS的历史数据缓存，同样保存在计算出它的参数服务器节点上。这使得运行大型模型（10亿级参数）成为现实，而且不会因传输参数和梯度过度集中在一个节点上而导致性能下降。 在典型的L-BFGS的并行实现中，数据被分布到许多机器上，每个机器负责对样本数据的一个特定的子集计算梯度，而后梯度值被传输回中心服务器（或者通过树形结构来聚合[16]）。因为许多方法都需要等待最慢的机器处理完毕，所以它并不能很好地扩展到大型共享集群中。为了解决该（扩展性）问题，我们采用了如下的负载均衡的方案：协调器分配给这N个模型副本一小部分的任务量，并且该计算任务远小于总批量，每当副本完成计算处于闲置状态时，立即给其分配新的计算任务，如此下去。为了在整个批量计算的最后阶段进一步优化慢速副本的任务处理，协调器调度最快结束的副本同时计算未完成的任务，从最先结束的副本处取得计算结果。该方案和MapReduce中的“备份任务”的使用相类似[24]。数据预取方式和通过将顺序数据传输到同一生产者以提高数据亲和性的方法一道，使得数据的获取不再是问题。和Downpour SGD中和参数服务器之间的高频率，高吞吐参数同步方式相反，Sandblaster中的计算者仅仅需在每次批处理的开始阶段获取参数，并且只需在极少的结束部分（用以免遭备份失效和重启）处需要传输梯度到参数服务器。

sandblaster.jpeg

实验

我们用两个不同的深度学习问题来衡量了我们设计的优化算法：(i)静态图像的物体识别和(ii)语音识别的声学处理。
语音识别任务是将一小段音频的中心区域（或帧）归类为数千种类型之一。我们使用了一个五层的深度网络：四个隐藏层，每个有2560个单元，并以sigmoid为激励函数；一个有8192个单元的softmax输出层。输入层是11个长度为25ms连续的相互重叠的语音，每个由40个对数动能值表示。层与层之间是全连接的，因此整个网络的参数数量有42M。我们用1.1G个弱标记样本集来训练模型，并且用保留的部分样本做测试集来衡量精确度。简单深度网络的配置和训练过程请参照[28]。
对于可视物体识别，我们训练了一个更大的局部区域连通的神经网络，并作用于ImageNet的有$1.6\times {10}^7$ 图像的数据集上，每个图像被缩放到100X100像素大小。整个网络有三个阶段，每个阶段都包含了过滤，池化，局部对比度归一化等操作，过滤层的每一个单元都和其前一层的10X10的小块图像相连接。我们的基础设施允许多个单元都和同一小块图像相连接，我们的实验中，同一连接单元数量从8增加到36不等。输出层由$2.1\times 10^4$个一对多模式的logistic分类器组成，每个分别代表ImageNet的一个物体种类。相似的深度网络配置和训练过程请参照[30]。

模型并行基准测试

为了测试DistBelief模型的并行性扩展，实验中以运行单个模型实例的划分（机器）数量作为变量，我们测量了用简单SGD训练处理单个mini-batch的平均时间。在图3中，我们通过计算训练的平均加速比来量化N个节点对并行化的影响：使用单个节点训练花费的时间对使用N个节点训练花费的时间的比值。模型中推断过程的加速比是相似的，因而没有显示出来。
中等大小的语音模型在8个机器节点上运行是最快的，相比于单个节点，加速比大约是2.2（每台机器配置其使用不超过20核CPU来训练模型）。将模型划分在大于8个机器节点上实际上会减缓训练过程，因为模型的全连通结构使得此时网络开销开始起决定性因素，同时节点的增加使得每个节点的计算量也相应地减少。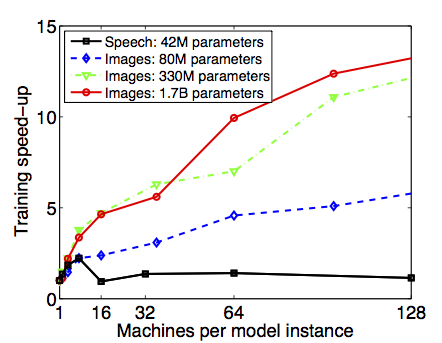
四个不同规模的深度网络使用单个DistBelief实例训练在集群机器不同规模下的加速比。具有较多参数的模型在机器增加时比较少参数模型获得更高的加速比
左图：采用不同的优化方法，在（在一部分训练集）上的训练精度。右图：训练时间的变化下，测试集的分类精度的变化曲线。Downpour SGD和Sandblaster实验均采用了10小时平凡SGD热启动方式来初始化。
相反地，比语音识别模型规模更大，且具有局部连通性的图像模型，能够通过持续给每个模型副本增加节点数量，来提升加速比。可以看出，具有$1.7\times 10^9$个参数的最大模型加速比最高，在使用了81个节点的情况下，获了12倍的加速比。对于大型模型来讲，通过持续增加机器数量始终能提升训练速度，但是获得的性能回报逐渐变少。
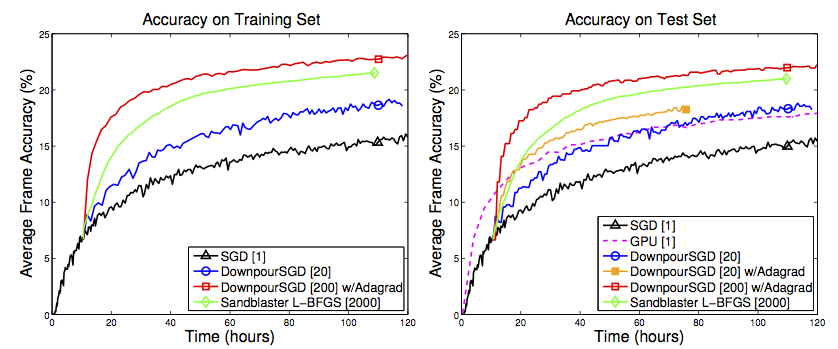
优化方法的比较：为了衡量提出的分布优化方式的性能，我们在不同的配置下，运行前面提及的语音模型。考虑两种基准方式（译者注：作为比较的靶对象）：(i)用传统（单个副本）SGD方法训练DistBelief模型（在8个划分上），(ii)用CUDA[28]在GPU上训练与(i)中同样的模型。三个和基准方式相比较的分布优化方法是：(i)固定学习速率的Downpour SGD，(ii)使用Adagrad自适应学习速率的Downpour SGD，(iii)Sandblaster L-BFGS。
图4说明了对于不同的优化方法，以训练时间作为分类的性能时的模型比较。我们的目标是忽略资源要求下，在最短的训练时间内，获得最佳的测试集分类精度。传统单副本的SGD（黑色曲线）是最慢速的。具有20个副本的Downpour SGD方法（蓝色曲线）在此基础上获得了显著的提升。20个副本的Downpour SGD和Adagrad相结合（橙色曲线）是可以被认为是中等速率的，而使用了2000个模型副本的Sandblaster L-BFGS更加快速（绿色曲线）。但是，最快的是200个模型副本并和Adagrad相结合的Downpour SGD方法（红色曲线）。可见，只要供给足够的CPU资源，Sandblaster L-BFGS和Downpour SGD方法对模型的训练都能从本质上快于高性能GPU。
尽管我们没有限制以上实验的资源使用，但是我们可以考虑这些优化方法是如何用硬件资源来换取性能提升的。将测试集精度设定为固定值（16%），在改变机器数量和CPU数量的条件下，测试上述方法达到该精度所需训练时间，以此方式来分析资源使用和性能的关系，如图5。每条曲线的四个点其中之一对应于图4中的训练配置，其他三个点是替代的配置。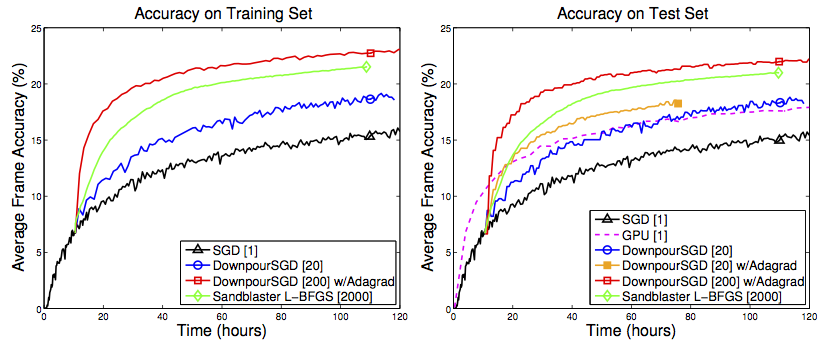
在不同机器数量（左图）和CPU数量（右图）下，几种优化策略达到固定精度值（16%）所花费的时间
在此坐标图中，距原点较近的点更优，因为它们在更少硬件资源的条件下，花费的训练时间更少。从这个角度上讲，使用Adagrad的Downpour SGD方法看起来是最好的权衡：对于任意固定机器数量或CPU数量条件下，该方法比Downpour SGD或Sandblaster L-BFGS花费更少的时间达到精度目标。对于任意给定达到精度目标的训练时间，使用Adagrad的Downpour SGD比Sandblaster L-BFGS使用更少的资源，并且在多数情况下，使用固定学习速率的Downpour SGD甚至都不能在最后期限内完成训练目标。Sandblaster L-BFGS看起来还能通过持续增加CPU数量来提高加速比，表明在极其大的（如3*10^4CPU使用量）资源使用条件下，应该会获得最快的训练时间。

应用到ImageNet

先前的实验证明了，我们的技术可以加速具有$10^7$参数数量的神经网络训练。但是，对于这些基于集群的分布式优化方法来讲，最有价值的优点，是它能扩展到远大于单个机器能够容纳得下的模型，更不用说单个GPU了。为了测试训练大型神经网络的能力，我们使用Downpour SGD训练了之前提及的具有$1.7\times 10^9$个参数的图像模型，用于分类任务。正如[30]中的细节描述，在ImageNet分类任务中，这个网络的训练结果获得了大约错误率15%交叉验证（Cross-Validation）的分类精度，比我们所已知的先前最高的精度提高了60%多。

结论

在这篇文章中，我们介绍了DistBelief，一个深度网络的分布并行训练的框架，并在该框架中发现了一些有效的分布优化策略。我们提出了Downpour SGD，一个高度异步的SGD变种算法，用以训练非凸的深度学习模型，其结果出乎意料的好。Sandblaster L-BFGS， L-BFGS的分布式实现，其与SGD相比具有竞争力。同时，对网络带宽的高效利用，使得其能够扩展到更大数量的并发线程来训练同一模型。这就是说，当具有2000数量CPU或更少时，Downpour SGD和Adagrad自适应学习速率方法的结合是最有效的方法。 Adagrad方法本身不是为异步SGD的使用而设计的，并且该方法最典型的应用也不是在非凸问题上。但是，在高度非线性的深度网络中，两者的结合的效果却如此的好。我们推测，在面对剧烈的异步更新时，Adagrad自动地对不稳定参数起到了稳定的效果，并且很自然地根据不同的深度网络层数的变化来调整学习速率。 实验结果表明，即使在中等规模的模型训练上，使用我们的大规模（分布式）方法，集群方法也比GPU要快，并且没有GPU对模型规模的限制。为了证明其训练更大模型的能力，我们通过训练一个超过10^9数量参数的模型，在ImageNet物体识别上获得了比先前最优的更好的精度水平。

References

  1. G. Dahl, D. Yu, L. Deng, and A. Acero. Context-dependent pre-trained deep neural networks for large vocabulary speech recognition. IEEE Transactions on Audio, Speech, and Language Processing, 2012.
  2. G. Hinton, L. Deng, D. Yu, G. Dahl, A. Mohamed, N. Jaitly, A. Senior, V. Vanhoucke, P. Nguyen, T. Sainath, and B. Kingsbury. Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Processing Magazine, 2012.
  3. D. C. Ciresan, U. Meier, L. M. Gambardella, and J. Schmidhuber. Deep big simple neural nets excel on handwritten digit recognition. CoRR, 2010.
  4. A. Coates, H. Lee, and A. Y. Ng. An analysis of single-layer networks in unsupervised feature learning. In AISTATS 14, 2011.
  5. Y. Bengio, R. Ducharme, P. Vincent, and C. Jauvin. A neural probabilistic language model. Journal of Machine Learning Research, 3:1137–1155, 2003.
  6. R. Collobert and J. Weston. A unified architecture for natural language processing: Deep neural networks with multitask learning. In ICML, 2008.
  7. Q. V. Le, J. Ngiam, A. Coates, A. Lahiri, B. Prochnow, and A. Y. Ng. On optimization methods for deep learning. In ICML, 2011.
  8. R. Raina, A. Madhavan, and A. Y. Ng. Large-scale deep unsupervised learning using graphics processors. In ICML, 2009.
  9. J. Martens. Deep learning via hessian-free optimization. In ICML, 2010.
  10. J. C. Duchi, E. Hazan, and Y. Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12:2121–2159, 2011.
  11. Q. Shi, J. Petterson, G. Dror, J. Langford, A. Smola, A. Strehl, and V. Vishwanathan. Hash kernels. In AISTATS, 2009.
  12. J. Langford, A. Smola, and M. Zinkevich. Slow learners are fast. In NIPS, 2009.
  13. G. Mann, R. McDonald, M. Mohri, N. Silberman, and D. Walker. Efficient large-scale distributed training of conditional maximum entropy models. In NIPS, 2009.
  14. R. McDonald, K. Hall, and G. Mann. Distributed training strategies for the structured perceptron. In NAACL, 2010.
  15. M. Zinkevich, M. Weimer, A. Smola, and L. Li. Parallelized stochastic gradient descent. In NIPS, 2010.
  16. A. Agarwal, O. Chapelle, M. Dudik, and J. Langford. A reliable effective terascale linear learning system. In AISTATS, 2011.
  17. A. Agarwal and J. Duchi. Distributed delayed stochastic optimization. In NIPS, 2011.
  18. C. H. Teo, Q. V. Le, A. J. Smola, and S. V. N. Vishwanathan. A scalable modular convex solver for regularized risk minimization. In KDD, 2007.
  19. F. Niu, B. Retcht, C. Re, and S. J. Wright. Hogwild! A lock-free approach to parallelizing stochastic gradient descent. In NIPS, 2011.
  20. J. Bergstra, O. Breuleux, F. Bastien, P. Lamblin, R. Pascanu, G. Desjardins, J. Turian, D. Warde-Farley, and Y. Bengio. Theano: a CPU and GPU math expression compiler. In SciPy, 2010.
  21. D. Ciresan, U. Meier, and J. Schmidhuber. Multi-column deep neural networks for image classification. Technical report, IDSIA, 2012.
  22. L. Deng, D. Yu, and J. Platt. Scalable stacking and learning for building deep architectures. In ICASSP, 2012.
  23. A. Krizhevsky. Learning multiple layers of features from tiny images. Technical report, U. Toronto, 2009.
  24. J. Dean and S. Ghemawat. Map-Reduce: simplified data processing on large clusters. CACM, 2008.
  25. Y. Low, J. Gonzalez, A. Kyrola, D. Bickson, C. Guestrin, and J. Hellerstein. Distributed GraphLab: A framework for machine learning in the cloud. In VLDB, 2012.
  26. L. Bottou. Stochastic gradient learning in neural networks. In Proceedings of Neuro-Nˆımes 91, 1991.
  27. Y. LeCun, L. Bottou, G. Orr, and K. Muller. Efficient backprop. In Neural Networks: Tricks of the trade. Springer, 1998.
  28. V. Vanhoucke, A. Senior, and M. Z. Mao. Improving the speed of neural networks on cpus. In Deep Learning and Unsupervised Feature Learning Workshop, NIPS 2011, 2011.
  29. J. Deng, W. Dong, R. Socher, L. -J. Li, K. Li, and L. Fei-Fei. ImageNet: A Large-Scale Hierarchical
  30. Image Database. In CVPR, 2009. 30. Q. V. Le, M. A. Ranzato, R. Monga, M. Devin, K. Chen, G. S. Corrado, J. Dean, and A. Y. Ng. Building high-level features using large scale unsupervised learning. In ICML, 2012.