推荐系统算法

基于统计的方法

基于人口学的推荐

基于人口统计学的推荐机制（Demographic-based Recommendation）是一种最易于实现的推荐方法，它只是简单的根据系统用户的基本信息发现用户的相关程度，然后将相似用户喜爱的其他物品推荐给当前用户。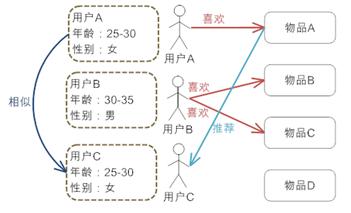

从图中可以很清楚的看到，首先，系统对每个用户都有一个用户 Profile 的建模，其中包括用户的基本信息，例如用户的年龄，性别等等；然后，系统会根据用户的 Profile 计算用户的相似度，可以看到用户 A 的 Profile 和用户 C 一样，那么系统会认为用户 A 和 C 是相似用户，在推荐引擎中，可以称他们是“邻居”；最后，基于“邻居”用户群的喜好推荐给当前用户一些物品，图中将用户 A 喜欢的物品 A 推荐给用户 C。

这种基于人口统计学的推荐机制的好处在于：

因为不使用当前用户对物品的喜好历史数据，所以对于新用户来讲没有“冷启动（Cold Start）”的问题。
这个方法不依赖于物品本身的数据，所以这个方法在不同物品的领域都可以使用，它是领域独立的（domain-independent）。

那么这个方法的缺点和问题是什么呢？这种基于用户的基本信息对用户进行分类的方法过于粗糙，尤其是对品味要求较高的领域，比如图书，电影和音乐等领域，无法得到很好的推荐效果。可能在一些电子商务的网站中，这个方法可以给出一些简单的推荐。另外一个局限是，这个方法可能涉及到一些与信息发现问题本身无关却比较敏感的信息，比如用户的年龄等，这些用户信息不是很好获取。

基于内容的推荐

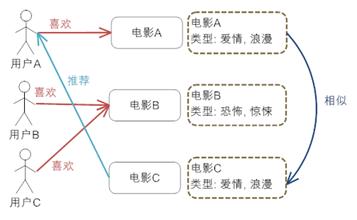
上图中给出了基于内容推荐的一个典型的例子，电影推荐系统，首先我们需要对电影的元数据有一个建模，这里只简单的描述了一下电影的类型；然后通过电影的元数据发现电影间的相似度，因为类型都是“爱情，浪漫”电影 A 和 C 被认为是相似的电影（当然，只根据类型是不够的，要得到更好的推荐，我们还可以考虑电影的导演，演员等等）；最后实现推荐，对于用户 A，他喜欢看电影 A，那么系统就可以给他推荐类似的电影 C。

这种基于内容的推荐机制的好处在于它能很好的建模用户的口味，能提供更加精确的推荐。但它也存在以下几个问题：

需要对物品进行分析和建模，推荐的质量依赖于对物品模型的完整和全面程度。在现在的应用中我们可以观察到关键词和标签（Tag）被认为是描述物品元数据的一种简单有效的方法。
物品相似度的分析仅仅依赖于物品本身的特征，这里没有考虑人对物品的态度。
因为需要基于用户以往的喜好历史做出推荐，所以对于新用户有“冷启动”的问题。

虽然这个方法有很多不足和问题，但他还是成功的应用在一些电影，音乐，图书的社交站点，有些站点还请专业的人员对物品进行基因编码，比如潘多拉，在一份报告中说道，在潘多拉的推荐引擎中，每首歌有超过 100 个元数据特征，包括歌曲的风格，年份，演唱者等等。

基于”邻域”的方法

基于用户相似的协同过滤算法

基于用户的协同过滤推荐算法拆分为两个步骤：

找到与目标用户兴趣相似的用户集合
找到这个集合中用户喜欢的、并且目标用户没有听说过的物品推荐给目标用户

发现兴趣相似的用户

通常用 Jaccard 公式或者余弦相似度计算两个用户之间的相似度。设 N(u) 为用户 u 喜欢的物品集合，N(v) 为用户 v 喜欢的物品集合，那么 u 和 v 的相似度是多少呢：
Jaccard 公式：
$$
w_{uv} = \frac{|N(u)\cap N(v)|}{|N(u)\cup N(v)|}
$$
余弦相似度：
$$
w_{uv} = \frac{|N(u)\cap N(v)|}{\sqrt{|N(u)\cup N(v)|}}
$$
假设目前共有4个用户： A、B、C、D；共有5个物品：a、b、c、d、e。用户与物品的关系（用户喜欢物品）如下图所示：

如何一下子计算所有用户之间的相似度呢？为计算方便，通常首先需要建立“物品—用户”的倒排表，如下图所示:

然后对于每个物品，喜欢他的用户，两两之间相同物品加1。例如喜欢物品 a 的用户有 A 和 B，那么在矩阵中他们两两加1。如下图所示：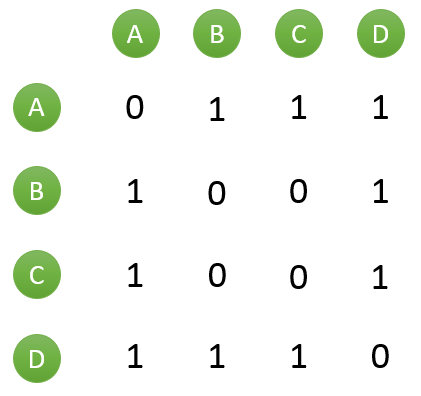

计算用户两两之间的相似度，上面的矩阵仅仅代表的是公式的分子部分。以余弦相似度为例，对上图进行进一步计算：

到此，计算用户相似度就大功告成，可以很直观的找到与目标用户兴趣较相似的用户。

对热门物品的改进

可以根据用户行为计算用户的兴趣相似度：
$$
w_{uv} = \frac{\sum_{i\in N(u) \cap N(v)}\frac{1}{log(1+|N(i)|)}}{|N(u)\cup N(v)|}
$$
该公式通过$\frac{1}{log(1+|N(i)|)}$惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响。

基于物品相似的协同过滤算法

基本思想是找出一个用户有过正反馈的物品的相似的物品来给其作为推荐：
算法可以拆分为两个步骤：

计算物品之间的相似度
根据物品的相似度和用户的历史行为给用户生成推荐列表

计算物品之间的相似度

我们定义物品的相似度，公式为
$$
w_{ij} = \frac{|N(i) \cap N(j)|}{|N(i)|}
$$
其中分母|N(i)|是喜欢物品i的用户数，而分子$|N(i) \cap N(j)|$是同时喜欢物品i和物品j的用户数。因此，公式可以理解为喜欢物品i的用户中有多少比例的用户也喜欢物品j。
同时，为了避免总推荐出热门的物品，可以用下面的公式：
$$
w_{ij} = \frac{|N(i) \cap N(j)|}{\sqrt{|N(i)||N(j)|}}
$$
假设用户A对物品a,b,d有过评价，用户B对物品b,c,e有过评价，如下图：

A : a b d
B : b c e
C : c d
D : b c d
E : a d
根据上面用户的行为构建:用户——物品倒排表：例如：物品a有用户A和E做过评价。
a : A E
b : A B D
c : B C D
d : A C D E
e : B
根据上面的倒排表我们可以构建一个相似度矩阵：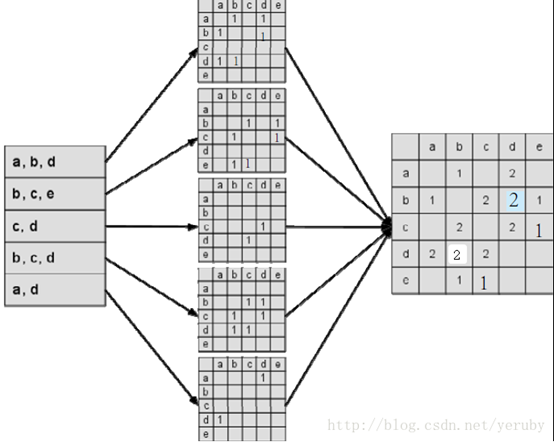

图中最左边的是用户输入的用户行为记录，每一行代表用户感兴趣的物品集合，然后对每个物品集合，我们将里面的物品两两加一，得到一个矩阵。最终将这些矩阵进行相加得到上面的C矩阵。其中C[i][j]记录了同时喜欢物品i和j的用户数。这样我们就得到了物品之间的相似度矩阵W。

根据物品的相似度和用户的历史行为记录给用户生成推荐列表

ItemCF通过下面的公式计算用户u对一个物品j的兴趣：
$$
p(u,j) = \sum_{i \in N(u) \cap S(j,k)}w_{ji}\times r_{ui}
$$
这里的N(u)代表用户喜欢的物品的集合，S(j,k)是和物品j最相似的的k个物品的集合，wij是物品j和i的相似度，r_ui代表用户u对物品i的兴趣。该公式的含义是，和用户历史上最感兴趣的物品月相似的物品，越有可能在用户的推荐列表中获得比较高的排名。

优化方法

（1）用户活跃度对物品相似度的影响
即认为活跃用户对物品相似度的贡献应该小于不活跃的用户，所以增加一个IUF（Inverse User Frequence）参数来修正物品相似度的计算公式：
$$
w_{ij} = \frac{\sum_{u \in N(i) \cap N(j)}\frac{1}{log(1+|N(u)|}}{\sqrt{|N(i)||N(j)|}}
$$
用这种相似度计算的ItemCF被记为ItemCF-IUF。
ItemCF-IUF在准确率和召回率两个指标上和ItemCF相近，但它明显提高了推荐结果的覆盖率，降低了推荐结果的流行度，从这个意义上说，ItemCF-IUF确实改进了ItemCF的综合性能。

（2）物品相似度的归一化
Karypis在研究中发现如果将ItemCF的相似度矩阵按最大值归一化，可以提高推荐的准确度。其研究表明，如果已经得到了物品相似度矩阵w，那么可用如下公式得到归一化之后的相似度矩阵w’：
$$
w’_{ij} = \frac{w_{ij}}{max_j{w_{ij}}}
$$
最终结果表明，归一化的好处不仅仅在于增加推荐的准确度，它还可以提高推荐的覆盖率和多样性。用这种相似度计算的ItemCF被记为ItemCF-Norm。

两种算法的比较

计算复杂度

Item CF 和 User CF 是基于协同过滤推荐的两个最基本的算法，User CF 是很早以前就提出来了，Item CF 是从 Amazon 的论文和专利发表之后（2001 年左右）开始流行，大家都觉得 Item CF 从性能和复杂度上比 User CF 更优，其中的一个主要原因就是对于一个在线网站，用户的数量往往大大超过物品的数量，同时物品的数据相对稳定，因此计算物品的相似度不但计算量较小，同时也不必频繁更新。但我们往往忽略了这种情况只适应于提供商品的电子商务网站，对于新闻，博客或者微内容的推荐系统，情况往往是相反的，物品的数量是海量的，同时也是更新频繁的，所以单从复杂度的角度，这两个算法在不同的系统中各有优势，推荐引擎的设计者需要根据自己应用的特点选择更加合适的算法。

适用场景

在非社交网络的网站中，内容内在的联系是很重要的推荐原则，它比基于相似用户的推荐原则更加有效。比如在购书网站上，当你看一本书的时候，推荐引擎会给你推荐相关的书籍，这个推荐的重要性远远超过了网站首页对该用户的综合推荐。可以看到，在这种情况下，Item CF 的推荐成为了引导用户浏览的重要手段。同时 Item CF 便于为推荐做出解释，在一个非社交网络的网站中，给某个用户推荐一本书，同时给出的解释是某某和你有相似兴趣的人也看了这本书，这很难让用户信服，因为用户可能根本不认识那个人；但如果解释说是因为这本书和你以前看的某本书相似，用户可能就觉得合理而采纳了此推荐。相反的，在现今很流行的社交网络站点中，User CF 是一个更不错的选择，User CF 加上社会网络信息，可以增加用户对推荐解释的信服程度。

总结

从上面的分析，可以很清晰的看到，这两种推荐都有其合理性，但都不是最好的选择，因此他们的精度也会有损失。其实对这类系统的最好选择是，如果系统给这个用户推荐 30 个物品，既不是每个领域挑选 10 个最热门的给他，也不是推荐 30 个 A 领域的给他，而是比如推荐 15 个 A 领域的给他，剩下的 15 个从 B,C 中选择。所以结合 User CF 和 Item CF 是最优的选择，结合的基本原则就是当采用 Item CF 导致系统对个人推荐的多样性不足时，我们通过加入 User CF 增加个人推荐的多样性，从而提高精度，而当因为采用 User CF 而使系统的整体多样性不足时，我们可以通过加入 Item CF 增加整体的多样性，同样同样可以提高推荐的精度。
用户对推荐算法的适应度
前面我们大部分都是从推荐引擎的角度考虑哪个算法更优，但其实我们更多的应该考虑作为推荐引擎的最终使用者 – 应用用户对推荐算法的适应度。
对于 User CF，推荐的原则是假设用户会喜欢那些和他有相同喜好的用户喜欢的东西，但如果一个用户没有相同喜好的朋友，那 User CF 的算法的效果就会很差，所以一个用户对的 CF 算法的适应度是和他有多少共同喜好用户成正比的。
Item CF 算法也有一个基本假设，就是用户会喜欢和他以前喜欢的东西相似的东西，那么我们可以计算一个用户喜欢的物品的自相似度。一个用户喜欢物品的自相似度大，就说明他喜欢的东西都是比较相似的，也就是说他比较符合 Item CF 方法的基本假设，那么他对 Item CF 的适应度自然比较好；反之，如果自相似度小，就说明这个用户的喜好习惯并不满足 Item CF 方法的基本假设，那么对于这种用户，用 Item CF 方法做出好的推荐的可能性非常低。

隐语义模型

SVD 原理

考虑CF中最为常见的用户给电影评分的场景，我们需要一个数学模型来模拟用户给电影打分的场景，比如对评分进行预测。

将评分矩阵U看作是两个矩阵的乘积：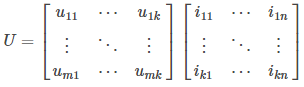

其中，u_{xy} 可以看作是user x对电影的隐藏特质y的热衷程度，而i_{yz}可以看作是特质y在电影z中的体现程度。那么上述模型的评分预测公式为：
$$
r’_{ui} = q_i^Tp_u
$$
q 和 p 分别对应了电影和用户在各个隐藏特质上的特征向量。
以上的模型中，用户和电影都体现得无差别，例如某些用户非常挑剔，总是给予很低的评分；或是某部电影拍得奇烂，恶评如潮。为了模拟以上的情况，需要引入 baseline predictor.
$$
r’_{ui} = \mu + b_u + b_i + q_i^T p_u
$$
其中$\mu$为所有评分基准，b_i 为电影 i 的评分均值相对$\mu$的偏移，b_u 类似。注意，这些均为参数，需要通过训练得到具体数值，不过可以用相应的均值作为初始化时的估计。

模型参数b_i,b_u,q_i,p_u通过最优化下面这个目标函数获得：
$$
min \sum_{(u,i)\in K}(r_{ui}-r’_{ui})^2+\lambda{\sum_u(b_u^2+||p_u||^2)}+\lambda{\sum_i(b_i^2+||q_i||^2)}
$$

使用隐因子的矩阵分解法

在矩阵分解法中，有一个假设，就是每一个用户都有一个长度为k的特征向量，每一部电影也有一个相同长度的特征向量（k一般需要用户指定）。那么所有用户的特征向量排列成一个矩阵 U 的维度为UserNum $\times$ k。其中用户i对应的向量为$U_i$。所有电影的特征向量排列成一个矩阵M 的维度为MoiveNum $\times$ k。其中电影j对应的向量为$U_j$。其中电影j对应的向量为$U_j$。那么用户i对电影j的评分 $V_ij = < U_i , M_j > $（$<>$代表点乘）。那么所有用户和所有电影之间的评分就可以用两个矩阵相乘来得到
$$
V’ = UM^T
$$
注意这里是$V’$而不是$V$。那么问题来了，我们如何确定这个U和M？一个自然的想法就是让$V’$和$V$尽可能地相等。那么这又有一个问题，那就是$V$（即数据集）有很多地方是没有评分的，如何判断$V$和$V’$是否相等？那么我们在这里只计算有评分处的MSE。这样既没有使用额外的信息，又能判断两者是否接近。那么自然而然得就引入了我们的lost function：
$$
E=\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^mI_{ij}(V_{ij}-p(U_i,M_j))^2 + \frac{k_u}{2}\sum_{i=1}^n||U_i||^2+\frac{k_m}{2}\sum_{i=1}^m||M_j||^2
$$
这里$I_{ij}$表示用户i对电影j有评分记录。后面两项是惩罚因子，目的是防止过拟合。

到这里我们就已经完成了基础的矩阵分解法。那么进一步，为了实现更好的效果，我们要考虑每个个体打分的影响，因为有些用户打分偏高，有些用户打分偏低。同样对于电影和所有的评分。所以我们评分的计算公式应该改为：
$$
V_{ij} =
< U_i,M_j> + mean + a_i +b_j
$$
　　其中mean是所有评分的平均值，$a_i$是用户i打分的平均值，$b_j$是电影j得分的平均值。其中mean认为是一个常数，而$a_i$和$b_j$都是需要优化的参数。

SVD++原理

SVD算法是指在SVD的基础上引入隐式反馈，使用用户的历史浏览数据、用户历史评分数据、电影的历史浏览数据、电影的历史评分数据等作为新的参数。某个用户对某个电影进行了评分，那么说明他看过这部电影，那么这样的行为事实上蕴含了一定的信息，因此我们可以这样来理解问题：评分的行为从侧面反映了用户的喜好，可以将这样的反映通过隐式参数的形式体现在模型中，从而得到一个更为精细的模型，便是 SVD++.
$$
r’_{ui} = \mu + b_u + b_i + q_i^T (p_u + \frac{1}{\sqrt{|N(u)|}}\sum_{j\in N(u)}y_{j})
$$
其中 N(u) 为该用户所评价过的所有电影的集合，yj为隐藏的“评价了电影 j”反映出的个人喜好偏置。
模型参数$b_i,b_u,q_i,p_u,y_j$通过最优化下面这个目标函数获得：
$$
min \sum_{(u,i)\in K}(r_{ui}-r’_{ui})^2+\lambda{\sum_u(b_u^2+||p_u||^2)}+\lambda{\sum_i(b_i^2+||q_i||^2+||y_i||^2)}
$$

与SVD方法类似，可以通过梯度下降算法进行求解。

SVM

其中线性SVM为：
$$
Y_{SVM} = w_0 + \sum_{i=1}^n w_ix_i
$$
如果使用多项式的核函数，以d=2为例，那么有:
$$
K(x, z) = ( < x, z > + 1 )^d
$$
因此，
$$
Y_{SVM} = w_0 + \sqrt{2}\sum_{i=1}^n w_ix_i + \sum_{i=1}^nw_{i,i}^{(2)}x_i^2 + \sqrt{2} \sum_{i=1}^n\sum_{j=1}^n w_{i,i}^{(2)}x_ix_j
$$
可以看到,d=2时的FM跟核函数为多项式的SVM形式相同，不同点在于SVM的$w_{i,j}$是完全没有关系的($w_{i,j}$与$w_{i,k}$),而在FM中$ < v_i, v_j > $ 与$ < v_i, v_k > $ 相关。

PITF(基于两两交互张量分解模型的个性化标签推荐)

为了形式化描述个性化标签推荐问题，我们使用数学符号：U为所有用户集合，I是所有产品集合，T是所有标签集合。历史标签信息由S⊆U×I×T给定。
我们的模型将用户、标签和产品之间的关系分解为两两交互的关系：
$$
y_{u,i,t} = w_0 + w_u + w_i + w_t + < v_u, v_i > + < v_u, v_t > + < v_t, v_i >
$$
因为给定的文章是同一篇，所以可以简化为：
$$
y_{u,i,t} = w_t + < v_u, v_t > + < v_t, v_i >
$$
因此可以看到，PITF与二值的FM是几乎相同的，不同点还是不同参数$ < v_i, v_j > $ 与$ < v_i, v_k > $ 是否相关的问题。

FPMC

状态转移+ 张量分解，请见基于个性化马尔科夫链的推荐算法

FM

FM（Factorization Machine）是由Konstanz大学Steffen Rendle（现任职于Google）于2010年最早提出的，旨在解决稀疏数据下的特征组合问题[7]。下面以一个示例引入FM模型。假设一个广告分类的问题，根据用户和广告位相关的特征，预测用户是否点击了广告。源数据如下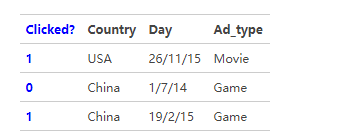

“Clicked?”是label，Country、Day、Ad_type是特征。由于三种特征都是categorical类型的，需要经过独热编码（One-Hot Encoding）转换成数值型特征。

由上表可以看出，经过One-Hot编码之后，大部分样本数据特征是比较稀疏的。上面的样例中，每个样本有7维特征，但平均仅有3维特征具有非零值。实际上，这种情况并不是此例独有的，在真实应用场景中这种情况普遍存在。例如，CTR/CVR预测时，用户的性别、职业、教育水平、品类偏好，商品的品类等，经过One-Hot编码转换后都会导致样本数据的稀疏性。特别是商品品类这种类型的特征，如商品的末级品类约有550个，采用One-Hot编码生成550个数值特征，但每个样本的这550个特征，有且仅有一个是有效的（非零）。由此可见，数据稀疏性是实际问题中不可避免的挑战。

One-Hot编码的另一个特点就是导致特征空间大。例如，商品品类有550维特征，一个categorical特征转换为550维数值特征，特征空间剧增。

同时通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。例如，“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为，而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的，如“化妆品”类商品与“女”性，“球类运动配件”的商品与“男”性，“电影票”的商品与“电影”品类偏好等。因此，引入两个特征的组合是非常有意义的。
多项式模型是包含特征组合的最直观的模型。在多项式模型中，特征 $x_i$ 和 $x_j$ 的组合采用 $x_ix_j$ 表示，即 $x_i$ 和 $x_j$ 都非零时，组合特征 $x_ix_j$ 才有意义。从对比的角度，本文只讨论二阶多项式模型。模型的表达式如下
$$
y(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^n\sum_{j=i+1}^nw_{ij}x_ix_j
$$
其中，n 代表样本的特征数量，$x_i$ 是第 i 个特征的值，$w_0$、$w_i$、$w_{ij}$ 是模型参数。
从公式(1)可以看出，组合特征的参数一共有 $\frac{n(n−1)}{2}$个，任意两个参数都是独立的。然而，在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的。其原因是，每个参数 $w_{ij}$ 的训练需要大量 $x_i$ 和 $x_j$ 都非零的样本；由于样本数据本来就比较稀疏，满足“$x_i$ 和 $x_j$ 都非零”的样本将会非常少。训练样本的不足，很容易导致参数 $w_{ij}$不准确，最终将严重影响模型的性能。

那么，如何解决二次项参数的训练问题呢？矩阵分解提供了一种解决思路。在model-based的协同过滤中，一个rating矩阵可以分解为user矩阵和item矩阵，每个user和item都可以采用一个隐向量表示[8]。比如在下图中的例子中，我们把每个user表示成一个二维向量，同时把每个item表示成一个二维向量，两个向量的点积就是矩阵中user对item的打分。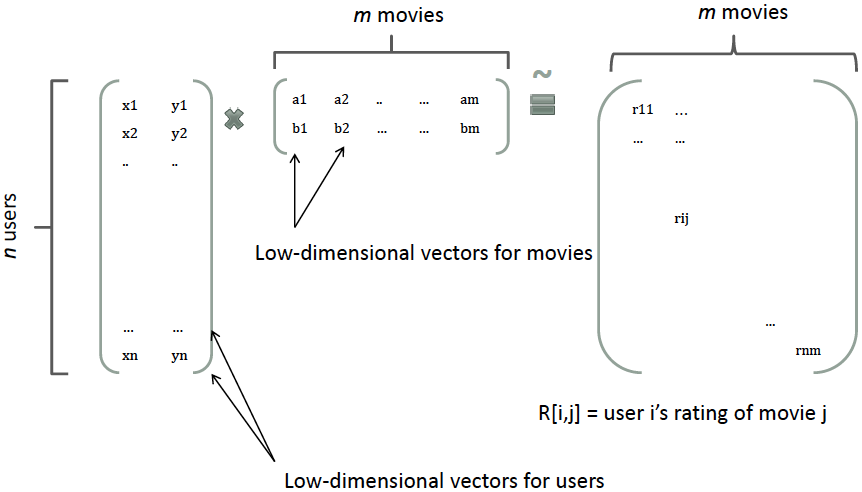

类似地，所有二次项参数 $w_{ij}$ 可以组成一个对称阵 W（为了方便说明FM的由来，对角元素可以设置为正实数），那么这个矩阵就可以分解为 $W=V^TV$，V 的第 j 列便是第 j 维特征的隐向量。换句话说，每个参数 $w_{ij} = < v_i, v_j >$，这就是FM模型的核心思想。因此，FM的模型方程为（本文不讨论FM的高阶形式）
$$
y(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^n\sum_{j=i+1}^n < v_i, v_j > x_ix_j
$$
其中，$v_i$ 是第 i 维特征的隐向量，<>代表向量点积。隐向量的长度为 $k（k << n）$，包含 k 个描述特征的因子。根据公式(2)，二次项的参数数量减少为 kn个，远少于多项式模型的参数数量。另外，参数因子化使得 $x_hx_i$ 的参数和$x_ix_j$ 的参数不再是相互独立的，因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说，$x_hx_i$和 $x_ix_j$的系数分别为 $< v_i, v_h > $和 $< v_i, v_j > $，它们之间有共同项 $v_i$。也就是说，所有包含“$x_i$ 的非零组合特征”（存在某个 j≠i，使得 $x_ix_j≠0$）的样本都可以用来学习隐向量 $v_i$，这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中，$w_{hi}$ 和 $w_{ij}$ 是相互独立的。

显而易见，公式(2)是一个通用的拟合方程，可以采用不同的损失函数用于解决回归、二元分类等问题，比如可以采用MSE（Mean Square Error）损失函数来求解回归问题，也可以采用Hinge/Cross-Entropy损失来求解分类问题。当然，在进行二元分类时，FM的输出需要经过sigmoid变换，这与Logistic回归是一样的。直观上看，FM的复杂度是 $O(kn^2)$。但是，通过公式(3)的等式，FM的二次项可以化简，其复杂度可以优化到 O(kn)[7]。由此可见，FM可以在线性时间对新样本作出预测。
$$
\sum_{i=1}^n\sum_{j=i+11}^n < v_i, v_j > x_ix_j = \frac{1}{2}\sum_{f=1}^k((\sum_{i=1}^nv_{i,f}x_i)^2-\sum_{i=1}^nv_{i,f}^2x_i^2)
$$

FM是一种比较灵活的模型，通过合适的特征变换方式，FM可以模拟二阶多项式核的SVM模型、MF模型、SVD++模型等。

相比SVM的二阶多项式核而言，FM在样本稀疏的情况下是有优势的；而且，FM的训练/预测复杂度是线性的，而二项多项式核SVM需要计算核矩阵，核矩阵复杂度就是N平方。

相比MF而言，我们把MF中每一项的rating分改写为$r_{ui}~\beta_u+\gamma_i+x^T_uy_i$ ，从公式(2)中可以看出，这相当于只有两类特征u 和i 的FM模型。对于FM而言，我们可以加任意多的特征，比如user的历史购买平均值，item的历史购买平均值等，但是MF只能局限在两类特征。SVD++与MF类似，在特征的扩展性上都不如FM，在此不再赘述。

FFM

原理

FFM（Field-aware Factorization Machine）最初的概念来自Yu-Chin Juan（阮毓钦，毕业于中国台湾大学，现在美国Criteo工作）与其比赛队员，是他们借鉴了来自Michael Jahrer的论文[14]中的field概念提出了FM的升级版模型。通过引入field的概念，FFM把相同性质的特征归于同一个field。以上面的广告分类为例，“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”这三个特征都是代表日期的，可以放到同一个field中。同理，商品的末级品类编码生成了550个特征，这550个特征都是说明商品所属的品类，因此它们也可以放到同一个field中。简单来说，同一个categorical特征经过One-Hot编码生成的数值特征都可以放到同一个field，包括用户性别、职业、品类偏好等。在FFM中，每一维特征 xixi，针对其它特征的每一种field fjfj，都会学习一个隐向量 $v_i,f_j$。因此，隐向量不仅与特征相关，也与field相关。也就是说，“Day=26/11/15”这个特征与“Country”特征和“Ad_type”特征进行关联的时候使用不同的隐向量，这与“Country”和“Ad_type”的内在差异相符，也是FFM中“field-aware”的由来。

假设样本的 n 个特征属于 f 个field，那么FFM的二次项有 nf个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看作FFM的特例，是把所有特征都归属到一个field时的FFM模型。根据FFM的field敏感特性，可以导出其模型方程。
$$
y(x)=w_0+\sum_{i=1}^nw_ix_i+\sum_{i=1}^n\sum_{j=i+1}^n < v_{i,f_j}, v_{j,f_i} > x_ix_j
$$
其中，$f_j$ 是第 j 个特征所属的field。如果隐向量的长度为 k，那么FFM的二次参数有 nfk个，远多于FM模型的 nk 个。此外，由于隐向量与field相关，FFM二次项并不能够化简，其预测复杂度是 $O(kn^2)$。
下面以一个例子简单说明FFM的特征组合方式[9]。输入记录如下

这条记录可以编码成5个特征，其中“Genre=Comedy”和“Genre=Drama”属于同一个field，“Price”是数值型，不用One-Hot编码转换。为了方便说明FFM的样本格式，我们将所有的特征和对应的field映射成整数编号。

应用

在DSP的场景中，FFM主要用来预估站内的CTR和CVR，即一个用户对一个商品的潜在点击率和点击后的转化率。

CTR和CVR预估模型都是在线下训练，然后用于线上预测。两个模型采用的特征大同小异，主要有三类：用户相关的特征、商品相关的特征、以及用户-商品匹配特征。用户相关的特征包括年龄、性别、职业、兴趣、品类偏好、浏览/购买品类等基本信息，以及用户近期点击量、购买量、消费额等统计信息。商品相关的特征包括所属品类、销量、价格、评分、历史CTR/CVR等信息。用户-商品匹配特征主要有浏览/购买品类匹配、浏览/购买商家匹配、兴趣偏好匹配等几个维度。

为了使用FFM方法，所有的特征必须转换成“field_id:feat_id:value”格式，field_id代表特征所属field的编号，feat_id是特征编号，value是特征的值。数值型的特征比较容易处理，只需分配单独的field编号，如用户评论得分、商品的历史CTR/CVR等。categorical特征需要经过One-Hot编码成数值型，编码产生的所有特征同属于一个field，而特征的值只能是0或1，如用户的性别、年龄段，商品的品类id等。除此之外，还有第三类特征，如用户浏览/购买品类，有多个品类id且用一个数值衡量用户浏览或购买每个品类商品的数量。这类特征按照categorical特征处理，不同的只是特征的值不是0或1，而是代表用户浏览或购买数量的数值。按前述方法得到field_id之后，再对转换后特征顺序编号，得到feat_id，特征的值也可以按照之前的方法获得。

CTR、CVR预估样本的类别是按不同方式获取的。CTR预估的正样本是站内点击的用户-商品记录，负样本是展现但未点击的记录；CVR预估的正样本是站内支付（发生转化）的用户-商品记录，负样本是点击但未支付的记录。构建出样本数据后，采用FFM训练预估模型，并测试模型的性能。

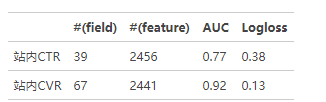
由于模型是按天训练的，每天的性能指标可能会有些波动，但变化幅度不是很大。这个表的结果说明，站内CTR/CVR预估模型是非常有效的。

在训练FFM的过程中，有许多小细节值得特别关注。

第一，样本归一化。FFM默认是进行样本数据的归一化，即 pa.norm 为真；若此参数设置为假，很容易造成数据inf溢出，进而引起梯度计算的nan错误。因此，样本层面的数据是推荐进行归一化的。

第二，特征归一化。CTR/CVR模型采用了多种类型的源特征，包括数值型和categorical类型等。但是，categorical类编码后的特征取值只有0或1，较大的数值型特征会造成样本归一化后categorical类生成特征的值非常小，没有区分性。例如，一条用户-商品记录，用户为“男”性，商品的销量是5000个（假设其它特征的值为零），那么归一化后特征“sex=male”（性别为男）的值略小于0.0002，而“volume”（销量）的值近似为1。特征“sex=male”在这个样本中的作用几乎可以忽略不计，这是相当不合理的。因此，将源数值型特征的值归一化到 [0,1][0,1] 是非常必要的。

第三，省略零值特征。从FFM模型的表达式(4)(4)可以看出，零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零，对于训练模型参数或者目标值预估是没有作用的。因此，可以省去零值特征，提高FFM模型训练和预测的速度，这也是稀疏样本采用FFM的显著优势。

参考

Factorization Machines
Factorization Machines with libFM
基于用户的协同过滤推荐算法原理和实现
 SVD++：推荐系统的基于矩阵分解的协同过滤算法的提高
 SVD与SVD++
推荐系统——基于隐因子矩阵分解的协同过滤算法
 基于两两交互张量分解模型的个性化标签推荐
 基于个性化马尔科夫链的推荐算法
深入FFM原理与实践

推荐算法概要