字符串全排列

发表于   |   分类于   |  

问题：给定字符串S，生成该字符串的全排列。
比如输入为abc，那么输出有以下几种：

1
abc acb bac bca cab cba

即如果输入字符串的长度为N的话，会输出N!个结果。
本文整理了求字符串全排列的若干方法。

方法1 使用STL库的标准函数

C++ STL中提供了std::next_permutation与std::prev_permutation可以获取数字或者是字符的全排列，其中std::next_permutation提供升序、std::prev_permutation提供降序。
1.std::next_permutation函数原型

1
2
3
4
　　template <class BidirectionalIterator>
　　bool next_permutation (BidirectionalIterator first, BidirectionalIterator last );
　　template <class BidirectionalIterator, class Compare>
　　bool next_permutation (BidirectionalIterator first,BidirectionalIterator last, Compare comp);

说明：next_permutation，重新排列范围内的元素[第一，最后一个）返回按照字典序排列的下一个值较大的组合。
返回值：如果有一个更高的排列，它重新排列元素，并返回true；如果这是不可能的（因为它已经在最大可能的排列），它按升序排列重新元素，并返回false。

1
2
3
4
5
6
7
8
9
10
11
12
#include <algorithm>
#include <string>
#include <iostream>
 
int main()
{
    std::string s = "aba";
    std::sort(s.begin(), s.end());
    do {
        std::cout << s << '\n';
    } while(std::next_permutation(s.begin(), s.end()));
}

方法2 仿STL库的标准函数实现

1
2
　[例]字符集{1,2,3},较小的数字较先,这样按字典序生成的全排列是:
     　　　　123,132,213,231,312,321

※ 一个全排列可看做一个字符串，字符串可有前缀、后缀。
生成给定全排列的下一个排列.所谓一个的下一个就是这一个与下一个之间没有其他的。这就要求这一个与下一个有尽可能长的共同前缀，也即变化限制在尽可能短的后缀上。

1
[例]839647521是1--9的排列。1—9的排列最前面的是123456789，最后面的987654321，从右向左扫描若都是增的，就到了987654321，也就没有下一个了。否则找出第一次出现下降的位置。

1
2
3
4
5
6
7
【例】 一般而言，设P是[1,n]的一个全排列。
　　　　　　P=P1P2…Pn=P1P2…Pj-1PjPj+1…Pk-1PkPk+1…Pn
　　　　find:　　j=max{i|Pi<Pi+1}
　　　　　　　　　k=max{i|Pi>Pj}
　　　　　　1，  对换Pj，Pk，
　　　　　　2，  将Pj+1…Pk-1PjPk+1…Pn翻转
         P’= P1P2…Pj-1PkPn…Pk+1PjPk-1…Pj+1即P的下一个

【例】 如何得到346987521的下一个

  1. 从尾部往前找第一个P(i-1) < P(i)的位置
    3 4 6 <- 9 <- 8 <- 7 <- 5 <- 2 <- 1
    最终找到6是第一个变小的数字，记录下6的位置i-1
  2. 从i位置往后找到最后一个大于6的数
    3 4 6 -> 9 -> 8 -> 7 5 2 1
    最终找到7的位置，记录位置为m
  3. 交换位置i-1和m的值
    3 4 7 9 8 6 5 2 1
  4. 倒序i位置后的所有数据
    3 4 7 1 2 5 6 8 9
    则347125689为346987521的下一个排列

依照上面的讲述不难将代码写出来，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
private static void PermutationList()
{
    int fromIndex, endIndex, changeIndex;
    Sort(0, length - 1);
    do
    {
        // 输出一种全排列
        Output();
        fromIndex = endIndex = length - 1;
        // 向前查找第一个变小的元素
        while (fromIndex > 0 && words[fromIndex] < words[fromIndex - 1]) --fromIndex;
        changeIndex = fromIndex;
        if (fromIndex == 0) break;
        // 向后查找最后一个大于words[fromIndex-1]的元素
        while (changeIndex + 1 < length && words[changeIndex + 1] > words[fromIndex - 1]) ++changeIndex;
        Swap(fromIndex - 1, changeIndex);   // 交换两个值
        InvertArray(fromIndex, endIndex);   // 对后面的所有值进行反向处理
    } while (true);
}

方法3 递归方法求全排列

　　递归方法很容易理解：分别将每个位置交换到最前面位，之后全排列剩下的位。

1
2
3
4
【例】递归全排列 1 2 3 4 5
    1. for循环将每个位置的数据交换到第一位
  		 swap(1,1~5)
	2. 按相同的方式全排列剩余的位

递归全排列1

由于递归方法很容易理解，而且网上也有很多的资料，所以不过多讲述，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/// <summary>
      /// 递归方式生成全排列的方法 3-1
      /// </summary>
      /// <param name="fromIndex">全排列的起始位置</param>
      /// <param name="endIndex">全排列的终止位置</param>
      private static void PermutationList(int fromIndex, int endIndex)
      {
          if (fromIndex == endIndex)
              Output();
          else
          {
              for (int index = fromIndex; index <= endIndex; ++index)
              {
                  //此处排序主要是为了生成字典序全排列，否则递归会打乱字典序
                  sort(fromIndex, endIndex);
                  Swap(fromIndex, index);
                  PermutationList(fromIndex + 1, endIndex);
                  Swap(fromIndex, index);
              }
          }
      }

不过需要注意,如果不加入第15行的sort(fromIndex, endIndex);那么生成的全排列就是非完全升序的.


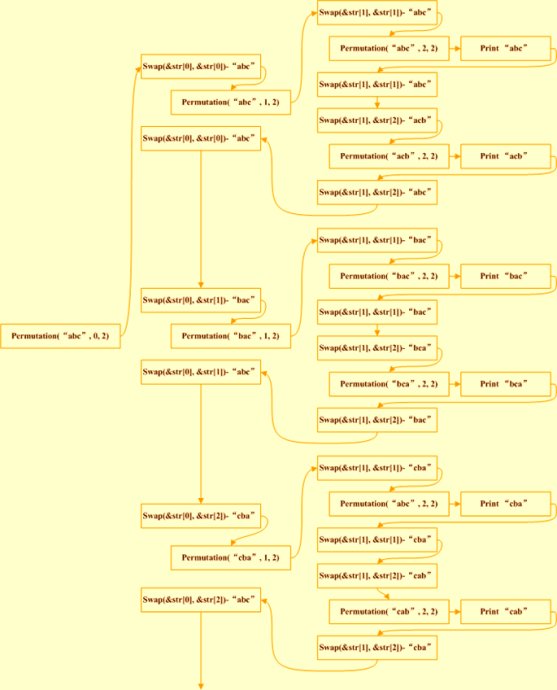
outorder-permutation.jpg

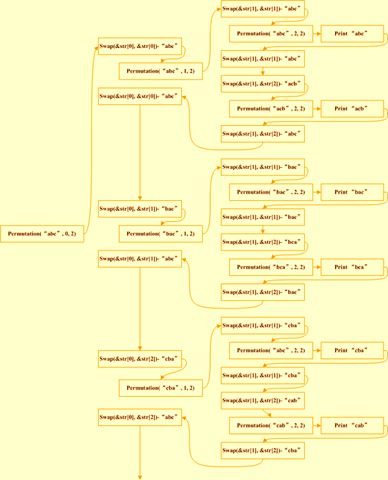
同时可以对进行修改,使其生成的全排列是完全升序的

递归全排列2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
using namespace std;
void p(char* str, int i, int size)
{
	//到达字符串末尾则停止并输出 
	if(i == size)
	{
		cout << str << endl;
	}
	for(int j = i; j < size; j++)
	{
		//置换; 
		for(int k = j; k > i; k--)
		{
			swap(str[k], str[k - 1]);
		}
		p(str, i + 1, size);
		//置换; 
		for(int k = i; k < j; k++)
		{
			swap(str[k], str[k + 1]);
		}
	}
	return;
}
int main()
{
	char str[7];
	cin >> str;
	int size = 0;
	//判断字符长度 
	for(int i = 0; i < 7; i++)
	{
		if(str[i] == '\0')
		{
			size = i;
			break;
		}
	}
	p(str, 0, size);
}

方法4 递归方法求全排列2

思路是这样的：我们维护两个序列，一个序列是要进行全排列的序列，我们暂称之为源序列，另一个序列是全排列之后的结果序列，我们称其为结果序列。过程如下：

  1. 初始时源序列为输入的字符串序列，结果序列为空

  2. 如果源序列中的元素个数大于1，则对源序列中的每一个元素，进行如下操作：

    1. 以结果序列+该元素生成新的结果序列
    2. 将该元素从源序列中剔除并保持其他元素顺序不变生成新的源序列

    然后以I产生的结果序列和II产生的源序列为基础递归2）过程

  3. 如果源序列中元素个数不大于1，则打印结果序列+源序列

下面给出了该思路的C++实现，参考[1][2]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void permutation(string begin, string end)
{
	int endLength = end.size(), beginLength = begin.size();
	if(endLength == 1)
	{
		cout << begin << end << endl;
		return ;
	}
	string newEnd;
	for(int i = 0; i < endLength; i++)
	{
		newEnd = end.substr(0, i) + end.substr(i+1);
		permutation(begin + end[i], newEnd);
	}
}
int main()
{
	string str;
	string n = "";
	cin >> str;
	permutation(n, str);
}


inorder-permutation.png

综上,文章介绍了四种字符串全排列的方法:

  • 去重: 方法1,方法2
  • 不去重按序：方法3-2,方法4
  • 不去重不排序：方法3-1

参考:

  1. Recursive method to find all permutations of a String
  2. 关于全排列算法的思考
  3. 字典序全排列算法研究